Ebener Spannungszustand - Hauptspannungen

3. Ebener Spannungszustand

Wiederholung der Kapiteleinleitung

Der ebene Spannungszustand (auch: zweiachsiger Spannungszustand, zweidimensionaler Spannungszustand) liegt dann vor, wenn eine zweidimensionale Belastung vorliegt.

Diese liegt an einem Element vor, das aus einer dünnen Scheibe herausgeschnitten wird und das nur in seiner Ebene belastet wird:

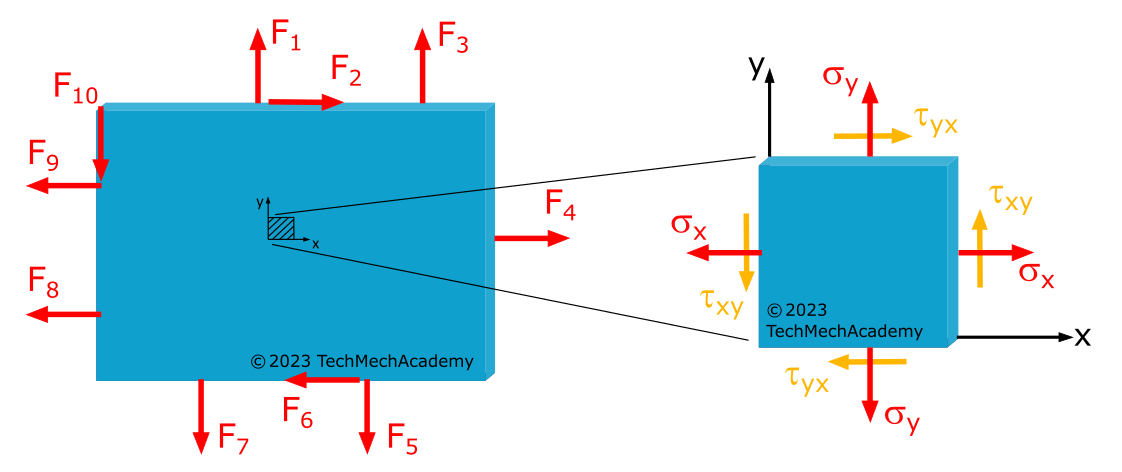
Diese Abbildung zeigt den ebenen Spannungszustand. — Abb. 1.3.1: Ebener Spannungszustand für eine x,y-Ebene

Die Abbildung 1.3.1 zeigt eine Scheibe, die in der $x$,$y$-Ebene belastet ist, in der $z$-Richtung tritt jedoch keine Belastung auf. Wir haben also eine lastfreie Oberfläche mit

$$ \begin{align} \tag{1} \sigma_z = \tau_{xz} = \tau_{zx} = \tau_{yz} = \tau_{zz}= 0 \end{align} $$

Natürlich könnte auch eine belastete $x$,$z$-Ebene vorliegen mit einer unbelasteten $y$-Achse oder eine belastete $y$,$z$-Ebene mit einer unbelasteten $z$-Achse. Die Orientierung des Koordinatensystems in der entsprechenden Ebene spielt dabei keine Rolle. Alle diese Fälle erfüllen eine der Bedingungen für das Vorliegen eines ebenen Spannungszustandes: Eine ebene Belastung mit lastfreier Oberfläche.

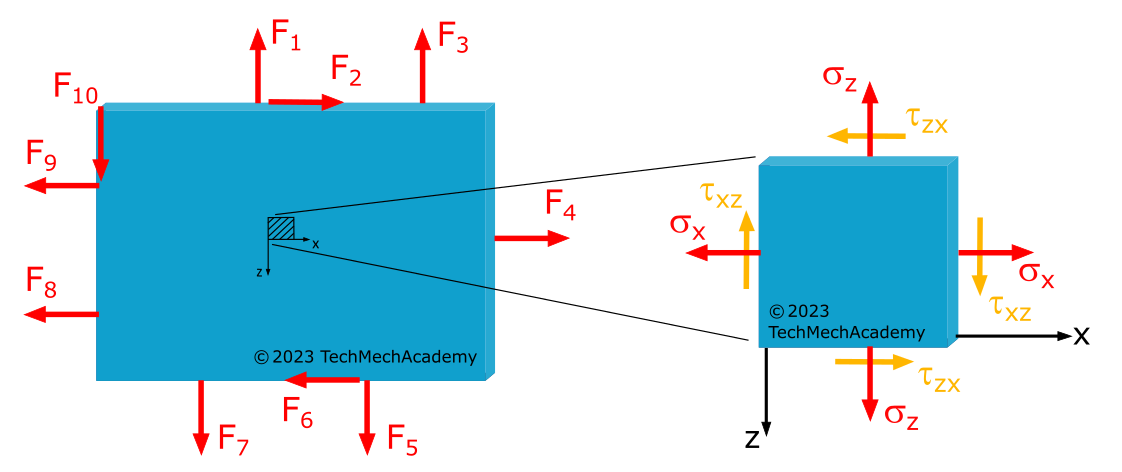
Eine weitere Bedingung für den ebenen Spannungszustand ist, dass die Dicke des Bauteils im Verhältnis zu seinen Längenabmessungen klein ist, also eine geringe Wandstärke vorhanden ist. Nur so können wir voraussetzen, dass die Spannungen $\sigma_x, \sigma_y$ und $\tau_{xy} = \tau_{yx}$ über die ganze Dicke der Scheibe gleichmäßig verteilt sind.

Nicht ganz klar, wo der Unterschied zwischen $\tau_{xy}$ und $\tau_{yx}$ bzw. $\tau_{xz}$ und $\tau_{zx}$ liegt? Schau bei der Indizierung der (Schub-)Spannungen nach.

Nicht ganz klar, warum $\tau_{xy} = \tau_{yx}$ bzw. $\tau_{xz} = \tau_{zx}$? Schau bei den zugeordneten Schubspannungen nach.

Nicht ganz klar, warum sich die Richtungen der Schubspannungen in den Abbildungen 1.3.1 und 1.3.2 unterscheiden? Schau bei der Vorzeichenfestlegung für Normal- und Schubspannungen nach.

3.2 Hauptspannungen

Im vorherigen Kapitel haben wir erarbeitet, wie wir aus den gegebenen Normal- und Schubspannungen $\sigma_x$, $\sigma_y$ und $\tau_{xy}=\tau_{yx}$ bzw. bei einer alternativ orientierten Ebene $\sigma_x$, $\sigma_z$ und $\tau_{xz}=\tau_{zx}$ für einen senkrechten Schnitt mithilfe der Transformationsgleichungen (1.7_xy) bzw. (1.7_xz) die Normalspannungen $\sigma_{\xi}$ und $\sigma_{\eta}$ sowie die Schubspannungen $\tau_{\xi\eta}=\tau_{\eta\xi}$ für einen beliebigen Schnittwinkel $\varphi$ berechnen können.

Zur Erinnerung: Letztlich ist es wichtig zu wissen, unter welchem Schnittwinkel $\varphi$ die größten oder auch die kleinsten Spannungen im untersuchten Punkt des Bauteils wirken und wie groß sie sind. Nur so können beispielsweise die Winkel von notwendigen Schweißnähten sinnvoll gewählt werden.

Die maximalen und minimalen Normalspannungen im untersuchten Punkt eines Bauteils heißen Hauptnormalspannungen oder auch Hauptspannungen. Wollen wir sie und die dazugehörigen Schnittwinkel $\varphi$ ermitteln, so können wir dies für die beiden verschiedenen Koordinatensysteme tun: Einmal für ein kartesisches Koordinatensystem, das eine Ebene beschreibt, in der die x-Achse in positiver Richtung nach rechts und die y-Achse in positiver Richtung nach oben zeigt und einmal für ein kartesisches Koordinatensystem, das eine Ebene beschreibt, in der die x-Achse in positiver Richtung nach rechts und die z-Achse in positiver Richtung nach unten zeigt:

Diese Abbildung zeigt einen vergleich zwischen einem x,y-Koordinatensystem und einem x,z-Koordinatensystem und den daraus resultierenden Richtungen der Schubspannungen. — Abb. 1.3.9: Vergleich der beschriebenen Koordinatensysteme

Wir müssen hier diese Unterscheidung vornehmen, weil die Richtung der Schubspannungen in der Ebene von der Wahl des Koordinatensystems abhängen. Dies liegt an der definierten Vorzeichenfestlegung für Normal- und Schubspannungen. In der Praxis reicht es aus, die Herleitung für ein bevorzugtes Koordinatensystem zu kennen und dessen Koordinatentransformation berechnen zu können. Da aber beide Systeme häufig verwendet werden, sollen an dieser Stelle beide Herleitungen gezeigt werden.

3.2.1 Bestimmung der Hauptspannungen für ein kartesisches Koordinatensystem mit positiver x-Achse nach rechts und positiver y-Achse nach oben

Diese Abbildung zeigt ein gedrehtes Koordinatensystem für den ebenen Spannungszustand. — Abb. 1.3.10: Bestimmung der Hauptspannungen: Gedrehtes Koordinatensystem für eine x,y-Ebene

Es ist nicht das Koordinatensystem, das dich interessiert? Überspringe diesen Abschnitt! Weiter zu: 3.2.2 Bestimmung der Hauptspannungen für ein kartesisches Koordinatensystem mit positiver x-Achse nach rechts und positiver z-Achse nach unten

Wir erreichen unser Ziel, indem wir die Extremwerte der beiden Gleichungen $\sigma_{\xi}(\varphi)$ und $\sigma_{\eta}(\varphi)$ aus der Formel (1.7_xy) bestimmen.

Dies erreichen wir durch Ableitung der Funktionen und Nullsetzen, da an den Extremstellen einer Funktion die Tangenten (= Ableitung) keine Steigung haben (= 0 sind).

Formel (1.7_xy):

$$ \begin{align} \tag{1} \sigma_{\xi} &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) + \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \cos(2\varphi) + \tau_{xy} \cdot \sin(2\varphi) \\[10pt] \tag{2} \sigma_{\eta} &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) - \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \cos(2\varphi) - \tau_{xy} \cdot \sin(2\varphi) \end{align} $$

Leiten wir also die Funktionen ab. Zunächst wenden wir die Summenregel an:

$$ \begin{align} \tag{3} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr)\biggr] + \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \cos(2\varphi)\biggr] + \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\tau_{xy} \cdot \sin(2\varphi)\biggr] \\[10pt] \tag{4} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr)\biggr] - \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \cos(2\varphi)\biggr] - \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\tau_{xy} \cdot \sin(2\varphi)\biggr] \end{align} $$

Die ersten Summanden aller Ableitungen sind Konstanten, deren Ableitung Null ist:

$$ \begin{align} \tag{5} \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr)\biggr] = 0 \end{align} $$

Bei den übrigen Summanden wenden wir die Faktorregel an. Wir erhalten also:

$$ \begin{align} \tag{6} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= 0 + \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\cos(2\varphi)\biggr] + \tau_{xy} \cdot \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\sin(2\varphi)\biggr] \\[10pt] \tag{7} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= 0 - \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\cos(2\varphi)\biggr] - \tau_{xy} \cdot \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\sin(2\varphi)\biggr] \end{align} $$

Die Ableitungen der trigonometrischen Funktionen $\sin$ und $\cos$ erhalten wir aus der Tabelle über Ableitungen von Grundfunktionen.

Da das Argument dieser Funktionen nicht nur einfach $\varphi$ ist, müssen wir zudem noch die Kettenregel anwenden:

$$ \begin{align} \tag{8} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= 0 + \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot (-) \sin(2\varphi) \cdot 2 + \tau_{xy} \cdot \cos(2\varphi) \cdot 2 \\[10pt] \tag{9} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= 0 - \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot (-) \sin(2\varphi) \cdot 2 - \tau_{xy} \cdot \cos(2\varphi) \cdot 2 \end{align} $$

Wir erhalten somit für das Koordinatensystem $x,y$ ($x$ nach rechts positiv, $y$ nach oben positiv) zwei Ableitungsfunktionen, die wir Null setzen, um die Stellen der Extremwerte zu erhalten (Steigung ist an diesen Stellen Null):

$$ \begin{align} \tag{10} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= - \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \sin(2\varphi) + 2 \cdot \tau_{xy} \cdot \cos(2\varphi) = 0 \\[10pt] \tag{11} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= + \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \sin(2\varphi) - 2 \cdot \tau_{xy} \cdot \cos(2\varphi) = 0 \end{align} $$

Wir teilen die Gleichungen durch $\cos(2\varphi)$, d.h. wir teilen jeden der Summanden der Gleichungen durch $\cos(2\varphi)$:

$$ \begin{align} \tag{12} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= - \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \dfrac{\sin(2\varphi)}{\cos(2\varphi)} + 2 \cdot \tau_{xy} = 0 \\[10pt] \tag{13} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= + \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \dfrac{\sin(2\varphi)}{\cos(2\varphi)} - 2 \cdot \tau_{xy} = 0 \end{align} $$

Mit $\dfrac{\sin(2\varphi)}{\cos(2\varphi)}= \tan(2\varphi)$ finalisieren wir die Gleichungen:

$$ \begin{align} \tag{14} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= - \bigl(\sigma_x - \sigma_y\bigr) \cdot \tan(2\varphi) + 2 \cdot \tau_{xy} = 0 \\[10pt] \tag{15} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= + \bigl(\sigma_x - \sigma_y\bigr) \cdot \tan(2\varphi) - 2 \cdot \tau_{xy} = 0 \end{align} $$

Wir stellen beide Gleichungen nach $\tan(2\varphi)$ um. Um klarzustellen, dass der Winkel $\varphi$ ein spezieller Winkel ist, nämlich der Schnittwinkel, unter dem die Hauptnormalspannungen auftreten, nennen wir ihn $\varphi^*$. Wir erhalten somit jeweils in beiden Fällen:

$$ \begin{aligned} \tan(2\varphi^*) &= \dfrac{2 \cdot \tau_{xy}}{\sigma_x - \sigma_y} \qquad \Rightarrow \qquad \varphi^* = \dfrac{1}{2}\arctan\Biggl(\dfrac{2 \cdot \tau_{xy}}{\sigma_x - \sigma_y}\Biggr) \end{aligned} $$

Beachte:

Wir erhalten also für die beiden Spannungen $\sigma_{\xi}(\varphi)$ und $\sigma_{\eta}(\varphi)$ des verwendeten Koordinatensystems Extremwerte für den gleichen Schnittwinkel $\varphi^*$.

Was bedeutet das konkret?

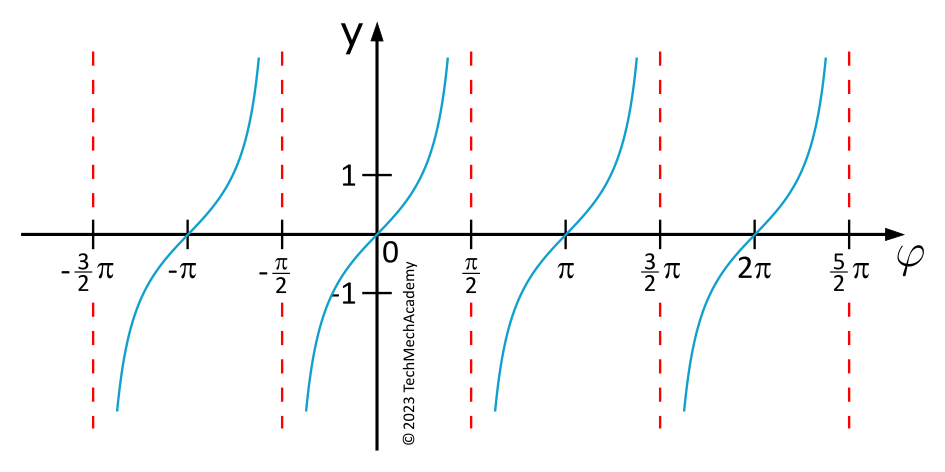
Diese Abbildung zeigt die Tangensfunktion. — Abb. 1.3.11: Tangensfunktion

Die Tangensfunktion ist periodisch mit einer Periode von $\pi$, d.h. die Tangensfunktion hat für alle $\varphi$, die sich um $\pi$ voneinander unterscheiden, den gleichen Wert.

Das Argument der Tangensfunktion der obigen Gleichung ist nicht einfach $\varphi^*$, sondern $2\varphi^*$.

Daher gilt hier:

$$ \begin{align} \tag{16} \tan(2\varphi^*) &= \tan(2\varphi^*\pm\pi) = \tan\biggl(2\Bigl(\varphi^*\pm\dfrac{\pi}{2}\Bigr)\biggr) \end{align} $$

Zur Erinnerung: $\dfrac{\pi}{2}$ im Bogenmaß entsprechen $90°$ im Gradmaß.

Diese Abbildung zeigt den Schnittwinkel Phi und die Winkel phi +90° und phi -90°. — Abb. 1.3.12: Schnittwinkel $\varphi^*$ und $\varphi^*\pm\dfrac{\pi}{2}$ im x,y-Koordinatensystem

Beachten wir, dass unsere bisherigen Überlegungen in diesem Kapitel für ein $x$,$y$-Koordinatensystem gelten, bei dem die positive $y$-Achse im Winkel $+\frac{\pi}{2}$ zur $x$-Achse angeordnet ist, bedeutet dies konkret:

Es gibt zwei senkrecht aufeinander stehende Schnittrichtungen $\varphi^*$ und $\varphi^* + \dfrac{\pi}{2}$, für welche die obige Gleichung erfüllt ist:

$$ \begin{aligned} \tan(2\varphi^*) &= \dfrac{2 \cdot \tau_{xy}}{\sigma_x - \sigma_y} \qquad \Rightarrow \qquad \varphi^* = \dfrac{1}{2}\arctan\Biggl(\dfrac{2 \cdot \tau_{xy}}{\sigma_x - \sigma_y}\Biggr), \qquad \varphi_{II}^* = \varphi^* + \dfrac{\pi}{2} \end{aligned} $$

(1.9_xy)

Diese Schnittrichtungen werden als Hauptschnittrichtungen bezeichnet.

Zu den beiden Hauptschnittrichtungen gehören also jeweils die maximale oder die minimale Normalspannung im untersuchten Punkt eines Bauteils.

Da die beiden Hauptschnittrichtungen in einem Winkel von $\frac{\pi}{2}$ bzw. $90°$ zueinander angeordnet sind, exisitiert ein Koordinatensystem, dessen Achsen zu den Hauptschnittrichtungen parallel sind.

Dieses Koordinatensystem wird als Hauptachsensystem bezeichnet.

Wir erhalten die zu den Hauptrichtungen gehörigen Hauptspannungen, indem wir die Gleichung (1.9_xy) mit der Gleichung (1.7_xy) koppeln.

Die Kopplung erfolgt, indem wir zunächst $\sin(2\varphi)$ und $\cos(2\varphi)$ der Gleichung (1.7_xy) durch die Gleichung (1.9_xy) mithilfe der Umrechnungen zwischen den Winkelfunktionen ersetzen.

Das ergibt für ein $x$,$y$-Koordinatensystem mit positiver $x$-Achse nach rechts und positiver $y$-Achse nach oben für $\sin(2\varphi)_{xy}$:

Alle Rechenschritte anzeigen

$$ \begin{align} \tag{17} sin(2\varphi)_{xy} &= \dfrac{\tan(2\varphi^*)}{\sqrt{1+\tan^2(2\varphi^*)}} \qquad \Biggr|~\text{Jetzt Gleichung 1.9xy einsetzen}\Biggl. \\[10pt] \tag{18} &= \dfrac{\dfrac{2 \cdot \tau_{xy}}{\sigma_x-\sigma_y}}{\sqrt{1+\Biggl(\dfrac{2 \cdot \tau_{xy}}{\sigma_x-\sigma_y}\Biggr)^2}} \\[10pt] \tag{19} &= \dfrac{\dfrac{2 \cdot \tau_{xy}}{\sigma_x-\sigma_y}}{\sqrt{\dfrac{(\sigma_x-\sigma_y)^2}{(\sigma_x-\sigma_y)^2}+\dfrac{(2 \cdot \tau_{xy})^2}{(\sigma_x-\sigma_y)^2}}}\\[10pt] \tag{20} &= \dfrac{\tau_{xy}}{\dfrac{\sigma_x-\sigma_y}{2}\sqrt{\dfrac{(\sigma_x-\sigma_y)^2+4 \tau_{xy}^2}{(\sigma_x-\sigma_y)^2} } }\\[10pt] \tag{21} &= \dfrac{\tau_{xy}}{\dfrac{\sigma_x-\sigma_y}{2} \cdot \dfrac{ \sqrt{(\sigma_x-\sigma_y)^2+4 \tau_{xy}^2}}{\sqrt{(\sigma_x-\sigma_y)^2}} }\\[10pt] \tag{22} &= \dfrac{\tau_{xy}}{\dfrac{\sigma_x-\sigma_y}{\sqrt{2^2}} \cdot \dfrac{ \sqrt{(\sigma_x-\sigma_y)^2+4 \tau_{xy}^2}}{\sigma_x-\sigma_y} }\\[10pt] \tag{23} &= \dfrac{\tau_{xy}}{\dfrac{\sqrt{(\sigma_x-\sigma_y)^2+4 \tau_{xy}^2}}{\sqrt{2^2}} } \\[10pt] \tag{24} &= \dfrac{\tau_{xy}}{\sqrt{ \dfrac{(\sigma_x-\sigma_y)^2}{2^2}+ \dfrac{4 \tau_{xy}^2}{2^2} }} \end{align} $$

$$ \begin{align} \tag{25} \sin(2\varphi)_{xy} &= \dfrac{\tau_{xy}}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} \end{align} $$

und für $\cos(2\varphi)_{xy}$:

Alle Rechenschritte anzeigen

$$ \begin{align} \tag{26} \cos(2\varphi)_{xy} &= \dfrac{1}{\sqrt{1+\tan^2(2\varphi^*)}} \qquad \Biggr|~\text{Jetzt Gleichung 1.9xy einsetzen}\Biggl. \\[10pt] \tag{27} &= \dfrac{1}{\sqrt{1+\Biggl(\dfrac{2 \cdot \tau_{xy}}{\sigma_x-\sigma_y}\Biggr)^2}} \\[10pt] \tag{28} &= \dfrac{1}{\sqrt{\dfrac{(\sigma_x-\sigma_y)^2}{(\sigma_x-\sigma_y)^2}+\dfrac{(2 \cdot \tau_{xy})^2}{(\sigma_x-\sigma_y)^2}}} \\[10pt] \tag{29} &= \dfrac{1}{\sqrt{\dfrac{(\sigma_x-\sigma_y)^2+4 \tau_{xy}^2}{(\sigma_x-\sigma_y)^2} } } \\[10pt] \tag{30} &= \dfrac{1}{\dfrac{ \sqrt{(\sigma_x-\sigma_y)^2+4 \tau_{xy}^2}}{\sqrt{(\sigma_x-\sigma_y)^2}} } \\[10pt] \tag{31} &= \dfrac{1}{\dfrac{ \sqrt{(\sigma_x-\sigma_y)^2+4 \tau_{xy}^2}}{\sigma_x-\sigma_y} } \\[10pt] \tag{32} &= \dfrac{\sigma_x-\sigma_y}{\sqrt{(\sigma_x-\sigma_y)^2+4 \tau_{xy}^2}} \\[10pt] \tag{33} &= \dfrac{\dfrac{1}{2} \cdot (\sigma_x-\sigma_y)}{\dfrac{1}{2} \cdot\sqrt{(\sigma_x-\sigma_y)^2+4 \tau_{xy}^2}} \\[10pt] \tag{34} &= \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)}{\dfrac{\sqrt{(\sigma_x-\sigma_y)^2+4 \tau_{xy}^2}}{\sqrt{2^2}}} \\[10pt] \tag{35} &= \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)}{\sqrt{ \dfrac{(\sigma_x-\sigma_y)^2}{2^2}+ \dfrac{4 \tau_{xy}^2}{2^2} }} \end{align} $$

$$ \begin{align} \tag{36} \cos(2\varphi)_{xy} &= \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} \end{align} $$

Jetzt können wir mit der Gleichung (1.7_xy) die Hauptspannungen bestimmen, indem wir $\sigma = \sigma_\xi(\varphi=\varphi^*)$ und $\sigma = \sigma_\eta(\varphi=\varphi^*)$ berechnen.

Das bedeutet für $\sigma = \sigma_\xi(\varphi=\varphi^*)$:

Alle Rechenschritte anzeigen

$$ \begin{align} \tag{37} \sigma &= \sigma_\xi(\varphi=\varphi^*) = \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) + \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \cos(2\varphi^*) + \tau_{xy} \cdot \sin(2\varphi^*) \\[10pt] \tag{38} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) + \dfrac{\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} + \dfrac{\tau_{xy}\cdot \tau_{xy}}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} \\[10pt] \tag{39} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) + \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr) \cdot \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr) + \tau_{xy}^2}{\sqrt{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} \\[10pt] \tag{40} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) + \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2 + \tau_{xy}^2}{\sqrt{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} \end{align} $$

Unter Anwendung des Potenzgesetzes für Potenzen mit gleicher Basis,

$$ \begin{align} \tag{41} \dfrac{a^m}{a^n} &= a^{m-n} \end{align} $$

und der Berücksichtung der Wurzelgesetze

$$ \begin{align} \tag{42} \sqrt[n]{a}&=a^{\frac{1}{n}} \\[7pt] \tag{43} \sqrt[2]{a}&=\sqrt{a} \end{align} $$

erhalten wir:

$$ \begin{align} \tag{44} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) + \dfrac{\biggl(\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2 + \tau_{xy}^2\biggr)^1}{\biggl(\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2\biggr)^{\frac{1}{2}}} \\[10pt] \tag{45} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) + \biggl(\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2\biggr)^{1-\frac{1}{2}} \end{align} $$

$$ \begin{aligned} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) + \sqrt{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2} \end{aligned} $$

Dies ist eine Formel für eine der beiden Hauptspannungen

Wollen wir die Hauptspannung über die Berechnung von $\sigma = \sigma_\eta(\varphi=\varphi^*)$ bestimmen, bedeutet das:

Alle Rechenschritte anzeigen

$$ \begin{align} \tag{46} \sigma &= \sigma_\eta(\varphi=\varphi^*) = \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) - \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \cos(2\varphi^*) - \tau_{xy} \cdot \sin(2\varphi^*) \\[10pt] \tag{47} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) - \dfrac{\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} - \dfrac{\tau_{xy}\cdot \tau_{xy}}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} \\[10pt] \tag{48} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) - \left[\dfrac{\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} + \dfrac{\tau_{xy}\cdot \tau_{xy}}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}}\right] \\[10pt] \tag{49} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) - \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr) \cdot \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr) + \tau_{xy}^2}{\sqrt{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} \\[10pt] \tag{50} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) - \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2 + \tau_{xy}^2}{\sqrt{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} \end{align} $$

Unter Anwendung des Potenzgesetzes für Potenzen mit gleicher Basis,

$$ \begin{align} \tag{51} \dfrac{a^m}{a^n} &= a^{m-n} \end{align} $$

und der Berücksichtung der Wurzelgesetze

$$ \begin{align} \tag{52} \sqrt[n]{a}&=a^{\frac{1}{n}} \\[7pt] \tag{53} \sqrt[2]{a}&=\sqrt{a} \end{align} $$

erhalten wir:

$$ \begin{align} \tag{54} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) - \dfrac{\biggl(\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2 + \tau_{xy}^2\biggr)^1}{\biggl(\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2 + \tau_{xy}^2\biggr)^{\frac{1}{2}}} \\[10pt] \tag{55} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) - \biggl(\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2 + \tau_{xy}^2\biggr)^{1-\frac{1}{2}} \end{align} $$

$$ \begin{aligned} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) - \sqrt{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2 + \tau_{xy}^2} \end{aligned} $$

Dies ist eine Formel für eine der beiden Hauptspannungen

Bleibt noch die Frage, wie groß die Schubspannungen unter den Hauptschnittrichtungen $\varphi^*$ und $\varphi_{II}^*$ sind.

Setzen wir die oben ermittelten

$$ \begin{align} \tag{56} \sin(2\varphi)_{xy} &= \dfrac{\tau_{xy}}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} \end{align} $$

und

$$ \begin{align} \tag{57} \cos(2\varphi)_{xy} &= \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} \end{align} $$

in die Gleichung für $\tau_{\xi\eta}$ nach (1.7_xy) ein, so erhalten wir:

$$ \begin{align} \tag{58} \tau &= \tau_{\xi\eta}(\varphi=\varphi^*) = - \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \sin(2\varphi) + \tau_{xy} \cdot \cos(2\varphi) \\[10pt] \tag{59} \tau &= - \dfrac{\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \tau_{xy} }{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} + \dfrac{\tau_{xy}\cdot \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2+ \tau_{xy}^2}} \\[10pt] \tag{60} \tau &= 0 \end{align} $$

Das bedeutet:

Die Schubspannungen verschwinden in den Hauptschnittrichtungen, in denen die Normalspannungen Extremwerte annehmen!

Zusammenfassend lauten also für ein kartesisches Koordinatensystem, das eine Ebene beschreibt, in der die x-Achse in positiver Richtung nach rechts und die y-Achse in positiver Richtung nach oben zeigt die Gleichungen für die Hauptspannungen des ebenen Spannungszustandes

$$ \begin{aligned} \sigma_{1,2} &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) \pm \sqrt{\Bigl(\dfrac{\sigma_x-\sigma_y}{2}\Bigr)^2 + \tau_{xy}^2}\\[7pt] &\qquad\text{wobei}\\[7pt] \tau_{12} &= \tau_{21} = 0 \end{aligned} $$

(1.10_xy)

Die Hauptspannungen können positiv oder negativ sein, je nachdem ob sie auf Zug oder Druck hinweisen. Die Indizes der Hauptspannungen sind so zu wählen, dass sie in absteigender Reihenfolge ihrer Größe sortiert sind, beginnend mit der größten Hauptspannung. Es gilt also

$$ \begin{align} \tag{61} \sigma_1 &> \sigma_2 \end{align} $$

Anmerkung:

Die mit Hilfe der Gleichung (1.9_xy) errechneten Winkel $\varphi^*$ und $\varphi_{II}^*$ dürfen nicht anhand ihrer Indizes den Hauptspannungen $\sigma_1$ und $\sigma_2$ zugeordnet werden! So kann der Winkel $\varphi^*$ der Richtungswinkel zwischen der $x$-Achse und der ersten oder der zweiten Hauptspannungsrichtung sein (siehe Abbildung 1.3.12).

Die Zuordnung der beiden Winkel $\varphi^*$ und $\varphi_{II}^* = \varphi^*+\frac{\pi}{2}$ zu den Hauptspannungen $\sigma_1$ und $\sigma_2$ erfolgt in der Regel dadurch, dass man den Winkel $\varphi^*$ in die erste Gleichung für $\sigma_\xi$ aus der Formel (1.7_xy) einsetzt.

Die dadurch berechnete Normalspannung ist entweder $\sigma_1$ oder $\sigma_2$ und man hat die dieser Normalspannung zugeordneten Schnittrichtung $\varphi_1^* = \varphi^*$ oder $\varphi_2^* = \varphi^*$ gefunden.

Beispiel 1.2: Größe und Richtung der Hauptspannungen bestimmen

In einem Blech seien die Spannungen $\sigma_x = 20\mathrm{~MPa}$, $\sigma_y = 30\mathrm{~MPa}$ und $\tau_{xy} = 10\mathrm{~MPa}$ gegeben.

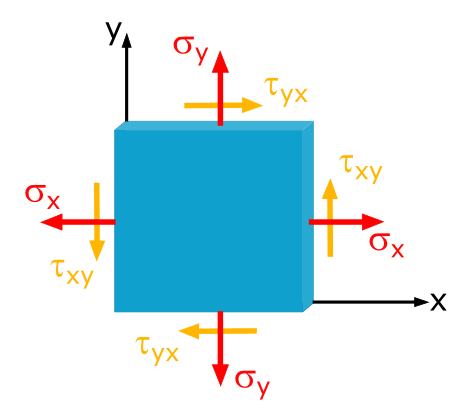
Blech mit gegebenen Spannungen. — Abb. B1.2: Blech mit gegebenen Spannungen

Bestimme die Größe und Richtung der Hauptspannungen.

Lösung

Für das gegebene $x$, $y$-Koordinatensystem, das eine Ebene beschreibt, in der die x-Achse in positiver Richtung nach rechts und die y-Achse in positiver Richtung nach oben zeigt und den gegebenen Spannungen $\sigma_x$, $\sigma_y$ und $\tau_{xy}$ können wir zur Bestimmmung der Hauptspannungen die Formel 1.10_xy anwenden:

Weiterlesen mit TechMechAcademy+

Alles. Immer. Überall.

Mit TechMechAcademy+ vollen Zugriff auf alle Inhalte.

Werde ein TechMechAcademy+ Premiummitglied!

Bist du bereits ein TechMechAcademy+ Premiummitglied? Dann logge dich bitte hier ein, um den vollen Zugriff auf alle Inhalte zu genießen.

3.2.2 Bestimmung der Hauptspannungen für ein kartesisches Koordinatensystem mit positiver x-Achse nach rechts und positiver z-Achse nach unten

Wir erreichen unser Ziel, indem wir die Extremwerte der beiden Gleichungen $\sigma_{\xi}(\varphi)$ und $\sigma_{\eta}(\varphi)$ aus der Formel (1.7_xz) bestimmen.

Dies erreichen wir durch Ableitung der Funktionen und Nullsetzen, da an den Extremstellen einer Funktion die Tangenten (= Ableitung) keine Steigung haben (= 0 sind).

Formel (1.7_xz):

$$ \begin{align} \tag{62} \sigma_{\xi} &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) + \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \cos(2\varphi) - \tau_{xz} \cdot \sin(2\varphi) \\[10pt] \tag{63} \sigma_{\eta} &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) - \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \cos(2\varphi) + \tau_{xz} \cdot \sin(2\varphi) \end{align} $$

Leiten wir also die Funktionen ab. Zunächst wenden wir die Summenregel an:

$$ \begin{align} \tag{64} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr)\biggr] + \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \cos(2\varphi)\biggr] - \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\tau_{xz} \cdot \sin(2\varphi)\biggr] \\[10pt] \tag{65} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr)\biggr] - \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \cos(2\varphi)\biggr] + \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\tau_{xz} \cdot \sin(2\varphi)\biggr] \end{align} $$

Die ersten Summanden aller Ableitungen sind Konstanten, deren Ableitung Null ist:

$$ \begin{align} \tag{66} \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr)\biggr] = 0 \end{align} $$

Bei den übrigen Summanden wenden wir die Faktorregel an. Wir erhalten also:

$$ \begin{align} \tag{67} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= 0 + \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\cos(2\varphi)\biggr] - \tau_{xz} \cdot \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\sin(2\varphi)\biggr] \\[10pt] \tag{68} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= 0 - \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\cos(2\varphi)\biggr] + \tau_{xz} \cdot \dfrac{\mathrm{d}}{\mathrm{d}\varphi}\biggl[\sin(2\varphi)\biggr] \end{align} $$

Die Ableitungen der trigonometrischen Funktionen $\sin$ und $\cos$ erhalten wir aus der Tabelle über Ableitungen von Grundfunktionen.

Da das Argument dieser Funktionen nicht nur einfach $\varphi$ ist, müssen wir zudem noch die Kettenregel anwenden:

$$ \begin{align} \tag{69} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= 0 + \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot (-) \sin(2\varphi) \cdot 2 - \tau_{xz} \cdot \cos(2\varphi) \cdot 2 \\[10pt] \tag{70} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= 0 - \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot (-) \sin(2\varphi) \cdot 2 + \tau_{xz} \cdot \cos(2\varphi) \cdot 2 \end{align} $$

Wir erhalten somit für das Koordinatensystem $x,z$ ($x$ nach rechts positiv, $z$ nach unten positiv) zwei Ableitungsfunktionen, die wir Null setzen, um die Stellen der Extremwerte zu erhalten (Steigung ist an diesen Stellen Null):

$$ \begin{align} \tag{71} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= - \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \sin(2\varphi) - 2 \cdot \tau_{xz} \cdot \cos(2\varphi) = 0 \\[10pt] \tag{72} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= + \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \sin(2\varphi) + 2 \cdot \tau_{xz} \cdot \cos(2\varphi) = 0 \end{align} $$

Wir teilen die Gleichungen durch $\cos(2\varphi)$, d.h. wir teilen jeden der Summanden der Gleichungen durch $\cos(2\varphi)$:

$$ \begin{align} \tag{73} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= - \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \dfrac{\sin(2\varphi)}{\cos(2\varphi)} - 2 \cdot \tau_{xz} = 0 \\[10pt] \tag{74} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= + \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \dfrac{\sin(2\varphi)}{\cos(2\varphi)} + 2 \cdot \tau_{xz} = 0 \end{align} $$

Mit $\dfrac{\sin(2\varphi)}{\cos(2\varphi)}= \tan(2\varphi)$ finalisieren wir die Gleichungen:

$$ \begin{align} \tag{75} \dfrac{\mathrm{d}\sigma_{\xi}}{\mathrm{d}\varphi} &= - \bigl(\sigma_x - \sigma_z\bigr) \cdot \tan(2\varphi) - 2 \cdot \tau_{xz} = 0 \\[10pt] \tag{76} \dfrac{\mathrm{d}\sigma_{\eta}}{\mathrm{d}\varphi} &= + \bigl(\sigma_x - \sigma_z\bigr) \cdot \tan(2\varphi) + 2 \cdot \tau_{xz} = 0 \end{align} $$

Wir stellen beide Gleichungen nach $\tan(2\varphi)$ um. Um klarzustellen, dass der Winkel $\varphi$ ein spezieller Winkel ist, nämlich der Schnittwinkel, unter dem die Hauptnormalspannungen auftreten, nennen wir ihn $\varphi^*$. Wir erhalten somit jeweils in beiden Fällen:

$$ \begin{aligned} \tan(2\varphi^*) &= -\dfrac{2 \cdot \tau_{xz}}{\sigma_x - \sigma_z} \qquad \Rightarrow \qquad \varphi^* = \dfrac{1}{2}\arctan\Biggl(-\dfrac{2 \cdot \tau_{xz}}{\sigma_x - \sigma_z}\Biggr) \end{aligned} $$

Beachte:

Wir erhalten also für die beiden Spannungen $\sigma_{\xi}(\varphi)$ und $\sigma_{\eta}(\varphi)$ des verwendeten Koordinatensystems Extremwerte für den gleichen Schnittwinkel $\varphi^*$.

Was bedeutet das konkret?

Die Tangensfunktion ist periodisch mit einer Periode von $\pi$, d.h. die Tangensfunktion hat für alle $\varphi$, die sich um $\pi$ voneinander unterscheiden, den gleichen Wert.

Das Argument der Tangensfunktion der obigen Gleichung ist nicht einfach $\varphi^*$, sondern $2\varphi^*$.

Daher gilt hier:

$$ \begin{align} \tag{77} \tan(2\varphi^*) &= \tan(2\varphi^*\pm\pi) = \tan\biggl(2\Bigl(\varphi^*\pm\dfrac{\pi}{2}\Bigr)\biggr) \end{align} $$

Zur Erinnerung: $\dfrac{\pi}{2}$ im entsprechen $90°$ im Gradmaß.

Beachten wir, dass unsere bisherigen Überlegungen in diesem Kapitel für ein $x$,$z$-Koordinatensystem gelten, bei dem die positive $z$-Achse im Winkel $-\frac{\pi}{2}$ zur $x$-Achse angeordnet ist, bedeutet dies konkret:

Es gibt zwei senkrecht aufeinander stehende Schnittrichtungen $\varphi^*$ und $\varphi^* - \dfrac{\pi}{2}$, für welche die obige Gleichung erfüllt ist:

$$ \begin{aligned} \tan(2\varphi^*) &= -\dfrac{2 \cdot \tau_{xz}}{\sigma_x - \sigma_z} \qquad \Rightarrow \qquad \varphi^* = \dfrac{1}{2}\arctan\Biggl(-\dfrac{2 \cdot \tau_{xz}}{\sigma_x - \sigma_z}\Biggr), \qquad \varphi_{II}^* = \varphi^* - \dfrac{\pi}{2} \end{aligned} $$

(1.9_xz)

Anmerkung:

An einigen Hochschulen ist es analog zur Berechnung der Hauptschnittrichtungen im $x$,$y$-Koordinatensystem gewünscht, $\varphi_{II}^* = \varphi^* \mathbf{+} \dfrac{\pi}{2}$ zu rechnen. Diese Schnittrichtung ist im Grunde mit der Schnittrichtung $\varphi_{II}^* = \varphi^* \mathbf{-} \dfrac{\pi}{2}$ äquivalent, da sie beide die gleiche Hauptschnittrichtung wie in Abbildung 1.3.15 gezeigt beschreiben.

Diese Schnittrichtungen werden als Hauptschnittrichtungen bezeichnet.

Zu den beiden Hauptschnittrichtungen gehören also jeweils die maximale oder die minimale Normalspannung im untersuchten Punkt eines Bauteils.

Da die beiden Hauptschnittrichtungen in einem Winkel von $\frac{\pi}{2}$ bzw. $90°$ zueinander angeordnet sind, exisitiert ein Koordinatensystem, dessen Achsen zu den Hauptschnittrichtungen parallel sind.

Dieses Koordinatensystem wird als Hauptachsensystem bezeichnet.

Wir erhalten die zu den Hauptrichtungen gehörigen Hauptspannungen, indem wir die Gleichung (1.9_xz) mit der Gleichung (1.7_xz) koppeln.

Die Kopplung erfolgt, indem wir zunächst $\sin(2\varphi)$ und $\cos(2\varphi)$ der Gleichung (1.7_xy) durch die Gleichung (1.9_xz) mithilfe der Umrechnungen zwischen den Winkelfunktionen ersetzen.

Das ergibt für ein $x$,$z$-Koordinatensystem mit positiver $x$-Achse nach rechts und positiver $z$-Achse nach unten für $\sin(2\varphi)_{xz}$:

Alle Rechenschritte anzeigen

$$ \begin{align} \tag{78} \sin(2\varphi)_{xz} &= \dfrac{\tan(2\varphi^*)}{\sqrt{1+\tan^2(2\varphi^*)}} \qquad \Biggr|~\text{Jetzt Gleichung 1.9xz einsetzen}\Biggl. \\[10pt] \tag{79} &= \dfrac{-\dfrac{2 \cdot \tau_{xz}}{\sigma_x-\sigma_z}}{\sqrt{1+\Biggl(-\dfrac{2 \cdot \tau_{xz}}{\sigma_x-\sigma_z}\Biggr)^2}} \\[10pt] \tag{80} &= \dfrac{-\dfrac{2 \cdot \tau_{xz}}{\sigma_x-\sigma_z}}{\sqrt{\dfrac{(\sigma_x-\sigma_z)^2}{(\sigma_x-\sigma_z)^2}+\dfrac{(-2 \cdot \tau_{xz})^2}{(\sigma_x-\sigma_z)^2}}}\\[10pt] \tag{81} &= \dfrac{-\tau_{xz}}{\dfrac{\sigma_x-\sigma_z}{2}\sqrt{\dfrac{(\sigma_x-\sigma_z)^2+4 \tau_{xz}^2}{(\sigma_x-\sigma_z)^2} } }\\[10pt] \tag{82} &= -\dfrac{\tau_{xz}}{\dfrac{\sigma_x-\sigma_z}{2} \cdot \dfrac{ \sqrt{(\sigma_x-\sigma_z)^2+4 \tau_{xz}^2}}{\sqrt{(\sigma_x-\sigma_z)^2}} }\\[10pt] \tag{83} &= -\dfrac{\tau_{xz}}{\dfrac{\sigma_x-\sigma_z}{\sqrt{2^2}} \cdot \dfrac{ \sqrt{(\sigma_x-\sigma_z)^2+4 \tau_{xz}^2}}{\sigma_x-\sigma_z} }\\[10pt] \tag{84} &= -\dfrac{\tau_{xz}}{\dfrac{\sqrt{(\sigma_x-\sigma_z)^2+4 \tau_{xz}^2}}{\sqrt{2^2}} } \\[10pt] \tag{85} &= -\dfrac{\tau_{xz}}{\sqrt{ \dfrac{(\sigma_x-\sigma_z)^2}{2^2}+ \dfrac{4 \tau_{xz}^2}{2^2} }} \end{align} $$

$$ \begin{align} \tag{86} \sin(2\varphi)_{xz} &= -\dfrac{\tau_{xz}}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \end{align} $$

und für $\cos(2\varphi)_{xz}$:

Alle Rechenschritte anzeigen

$$ \begin{align} \tag{87} \cos(2\varphi)_{xz} &= \dfrac{1}{\sqrt{1+\tan^2(2\varphi^*)}} \qquad \Biggr|~\text{Jetzt Gleichung 1.9xz einsetzen}\Biggl. \\[10pt] \tag{88} &= \dfrac{1}{\sqrt{1+\Biggl(-\dfrac{2 \cdot \tau_{xz}}{\sigma_x-\sigma_z}\Biggr)^2}} \\[10pt] \tag{89} &= \dfrac{1}{\sqrt{\dfrac{(\sigma_x-\sigma_z)^2}{(\sigma_x-\sigma_z)^2}+\dfrac{(-2 \cdot \tau_{xz})^2}{(\sigma_x-\sigma_z)^2}}} \\[10pt] \tag{90} &= \dfrac{1}{\sqrt{\dfrac{(\sigma_x-\sigma_z)^2+4 \tau_{xz}^2}{(\sigma_x-\sigma_z)^2} } } \\[10pt] \tag{91} &= \dfrac{1}{\dfrac{ \sqrt{(\sigma_x-\sigma_z)^2+4 \tau_{xz}^2}}{\sqrt{(\sigma_x-\sigma_z)^2}} } \\[10pt] \tag{92} &= \dfrac{1}{\dfrac{ \sqrt{(\sigma_x-\sigma_z)^2+4 \tau_{xz}^2}}{\sigma_x-\sigma_z} } \\[10pt] \tag{93} &= \dfrac{\sigma_x-\sigma_z}{\sqrt{(\sigma_x-\sigma_z)^2+4 \tau_{xz}^2}} \\[10pt] \tag{94} &= \dfrac{\dfrac{1}{2} \cdot (\sigma_x-\sigma_z)}{\dfrac{1}{2} \cdot\sqrt{(\sigma_x-\sigma_z)^2+4 \tau_{xz}^2}} \\[10pt] \tag{95} &= \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)}{\dfrac{\sqrt{(\sigma_x-\sigma_z)^2+4 \tau_{xz}^2}}{\sqrt{2^2}}} \\[10pt] \tag{96} &= \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)}{\sqrt{ \dfrac{(\sigma_x-\sigma_z)^2}{2^2}+ \dfrac{4 \tau_{xz}^2}{2^2} }} \end{align} $$

$$ \begin{align} \tag{97} \cos(2\varphi)_{xz} &= \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \end{align} $$

Jetzt können wir mit der Gleichung (1.7_xz) die Hauptspannungen bestimmen, indem wir $\sigma = \sigma_\xi(\varphi=\varphi^*)$ und $\sigma = \sigma_\eta(\varphi=\varphi^*)$ berechnen.

Das bedeutet für $\sigma = \sigma_\xi(\varphi=\varphi^*)$:

Alle Rechenschritte anzeigen

$$ \begin{align} \tag{98} \sigma &= \sigma_\xi(\varphi=\varphi^*) = \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) + \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \cos(2\varphi^*) - \tau_{xz} \cdot \sin(2\varphi^*) \\[10pt] \tag{99} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) + \dfrac{\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} - \dfrac{\tau_{xz}\cdot (-)\tau_{xz}}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \\[10pt] \tag{100} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) + \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr) \cdot \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr) + \tau_{xz}^2}{\sqrt{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \\[10pt] \tag{101} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) + \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2 + \tau_{xz}^2}{\sqrt{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \end{align} $$

Unter Anwendung des Potenzgesetzes für Potenzen mit gleicher Basis,

$$ \begin{align} \tag{102} \dfrac{a^m}{a^n} &= a^{m-n} \end{align} $$

und der Berücksichtung der Wurzelgesetze

$$ \begin{align} \tag{103} \sqrt[n]{a}&=a^{\frac{1}{n}} \\[7pt] \tag{104} \sqrt[2]{a}&=\sqrt{a} \end{align} $$

erhalten wir:

$$ \begin{align} \tag{105} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) + \dfrac{\biggl(\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2 + \tau_{xz}^2\biggr)^1}{\biggl(\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2\biggr)^{\frac{1}{2}}} \\[10pt] \tag{106} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) + \biggl(\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2\biggr)^{1-\frac{1}{2}} \end{align} $$

$$ \begin{aligned} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) + \sqrt{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2} \end{aligned} $$

Dies ist eine Formel für eine der beiden Hauptspannungen

Wollen wir die Hauptspannung über die Berechnung von $\sigma = \sigma_\eta(\varphi=\varphi^*)$ bestimmen, bedeutet das:

Alle Rechenschritte anzeigen

$$ \begin{align} \tag{107} \sigma &= \sigma_\eta(\varphi=\varphi^*) = \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) - \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \cos(2\varphi^*) + \tau_{xz} \cdot \sin(2\varphi^*) \\[10pt] \tag{108} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) - \dfrac{\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} + \dfrac{\tau_{xz}\cdot (-)\tau_{xz}}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \\[10pt] \tag{109} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) - \dfrac{\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} - \dfrac{\tau_{xz}\cdot \tau_{xz}}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \\[10pt] \tag{110} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) - \left[\dfrac{\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} + \dfrac{\tau_{xz}\cdot \tau_{xz}}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}}\right] \\[10pt] \tag{111} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) - \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr) \cdot \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr) + \tau_{xz}^2}{\sqrt{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \\[10pt] \tag{112} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) - \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2 + \tau_{xz}^2}{\sqrt{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \end{align} $$

Unter Anwendung des Potenzgesetzes für Potenzen mit gleicher Basis,

$$ \begin{align} \tag{113} \dfrac{a^m}{a^n} &= a^{m-n} \end{align} $$

und der Berücksichtung der Wurzelgesetze

$$ \begin{align} \tag{114} \sqrt[n]{a}&=a^{\frac{1}{n}} \\[7pt] \tag{115} \sqrt[2]{a}&=\sqrt{a} \end{align} $$

erhalten wir:

$$ \begin{align} \tag{116} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) - \dfrac{\biggl(\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2 + \tau_{xz}^2\biggr)^1}{\biggl(\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2 + \tau_{xz}^2\biggr)^{\frac{1}{2}}} \\[10pt] \tag{117} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) - \biggl(\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2 + \tau_{xz}^2\biggr)^{1-\frac{1}{2}} \end{align} $$

$$ \begin{aligned} \sigma &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) - \sqrt{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2 + \tau_{xz}^2} \end{aligned} $$

Dies ist eine Formel für eine der beiden Hauptspannungen

Bleibt noch die Frage, wie groß die Schubspannungen unter den Hauptschnittrichtungen $\varphi^*$ und $\varphi_{II}^*$ sind.

Setzen wir die oben ermittelten

$$ \begin{align} \tag{118} \sin(2\varphi)_{xz} &= -\dfrac{\tau_{xz}}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \end{align} $$

und

$$ \begin{align} \tag{119} \cos(2\varphi)_{xz} &= \dfrac{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \end{align} $$

in die Gleichung für $\tau_{\xi\eta}$ nach (1.7_xz) ein, so erhalten wir:

$$ \begin{align} \tag{120} \tau &= \tau_{\xi\eta}(\varphi=\varphi^*) = \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \sin(2\varphi) + \tau_{xz} \cdot \cos(2\varphi) \\[10pt] \tag{121} \tau &= \dfrac{\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot (-)\tau_{xz} }{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} + \dfrac{\tau_{xz}\cdot \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \\[10pt] \tag{122} \tau &= - \dfrac{\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \tau_{xz} }{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} + \dfrac{\tau_{xz}\cdot \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)}{\sqrt{ \Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2+ \tau_{xz}^2}} \\[10pt] \tag{123} \tau &= 0 \end{align} $$

Das bedeutet:

Die Schubspannungen verschwinden in den Hauptschnittrichtungen, in denen die Normalspannungen Extremwerte annehmen!

Zusammenfassend lauten also für ein kartesisches Koordinatensystem, das eine Ebene beschreibt, in der die x-Achse in positiver Richtung nach rechts und die z-Achse in positiver Richtung nach unten zeigt die Gleichungen für die Hauptspannungen des ebenen Spannungszustandes

$$ \begin{aligned} \sigma_{1,2} &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) \pm \sqrt{\Bigl(\dfrac{\sigma_x-\sigma_z}{2}\Bigr)^2 + \tau_{xz}^2}\\[7pt] &\qquad\text{wobei}\\[7pt] \tau_{12} &= \tau_{21} = 0 \end{aligned} $$

(1.10_xz)

Die Hauptspannungen können positiv oder negativ sein, je nachdem ob sie auf Zug oder Druck hinweisen. Die Indizes der Hauptspannungen sind so zu wählen, dass sie in absteigender Reihenfolge ihrer Größe sortiert sind, beginnend mit der größten Hauptspannung. Es gilt also

$$ \begin{align} \tag{124} \sigma_1 &> \sigma_2 \end{align} $$

Anmerkung:

Die mit Hilfe der Gleichung (1.9_xz) errechneten Winkel $\varphi^*$ und $\varphi_{II}^*$ dürfen nicht anhand ihrer Indizes den Hauptspannungen $\sigma_1$ und $\sigma_2$ zugeordnet werden! So kann der Winkel $\varphi^*$ der Richtungswinkel zwischen der $x$-Achse und der ersten oder der zweiten Hauptspannungsrichtung sein (siehe Abbildung 1.3.15).

Die Zuordnung der beiden Winkel $\varphi^*$ und $\varphi_{II}^* = \varphi^*-\frac{\pi}{2}$ zu den Hauptspannungen $\sigma_1$ und $\sigma_2$ erfolgt in der Regel dadurch, dass man den Winkel $\varphi^*$ in die erste Gleichung für $\sigma_\xi$ aus der Formel (1.7_xz) einsetzt.

Die dadurch berechnete Normalspannung ist entweder $\sigma_1$ oder $\sigma_2$ und man hat die dieser Normalspannung zugeordneten Schnittrichtung $\varphi_1^* = \varphi^*$ oder $\varphi_2^* = \varphi^*$ gefunden.

Beispiel 1.3: Größe und Richtung der Hauptspannungen bestimmen

In einem Blech seien die Spannungen $\sigma_x = 20\mathrm{~MPa}$, $\sigma_z = 30\mathrm{~MPa}$ und $\tau_{xz} = 10\mathrm{~MPa}$ gegeben.

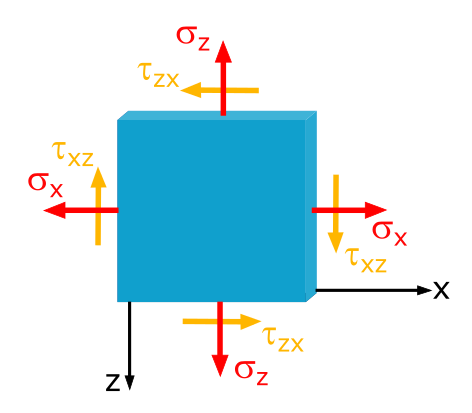
Bestimme die Größe und Richtung der Hauptspannungen.

Lösung

Für das gegebene $x$, $z$-Koordinatensystem, das eine Ebene beschreibt, in der die x-Achse in positiver Richtung nach rechts und die z-Achse in positiver Richtung nach unten zeigt und den gegebenen Spannungen $\sigma_x$, $\sigma_z$ und $\tau_{xz}$ können wir zur Bestimmmung der Hauptspannungen die Formel 1.10_xz anwenden: