Ebener Spannungszustand - Koordinatentransformation

3. Ebener Spannungszustand

Der ebene Spannungszustand (auch: zweiachsiger Spannungszustand, zweidimensionaler Spannungszustand) liegt dann vor, wenn eine zweidimensionale Belastung vorliegt.

Diese liegt an einem Element vor, das aus einer dünnen Scheibe herausgeschnitten wird und das nur in seiner Ebene belastet wird:

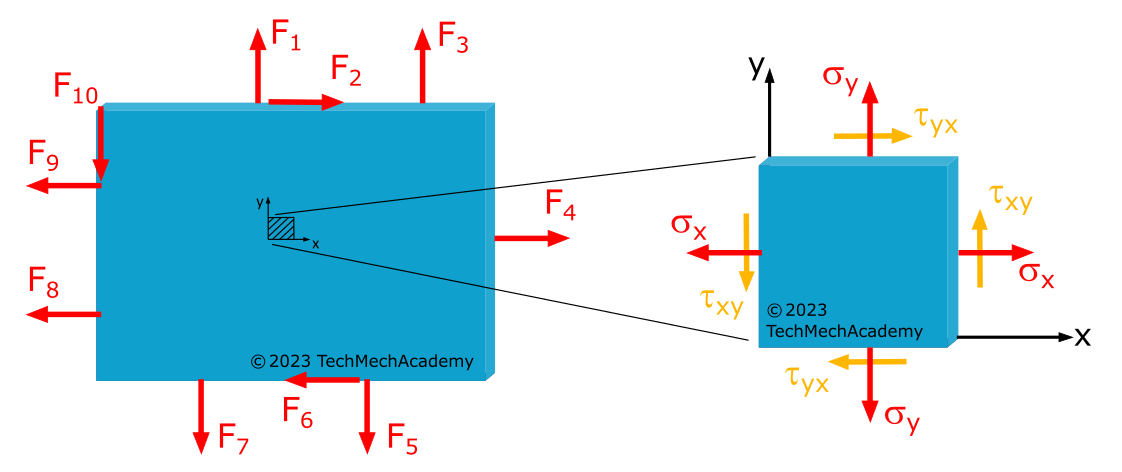
Diese Abbildung zeigt den ebenen Spannungszustand. — Abb. 1.3.1: Ebener Spannungszustand für eine x,y-Ebene

Die Abbildung 1.3.1 zeigt eine Scheibe, die in der $x$,$y$-Ebene belastet ist, in der $z$-Richtung tritt jedoch keine Belastung auf. Wir haben also eine lastfreie Oberfläche mit

$$ \begin{align} \tag{1} \sigma_z = \tau_{xz} = \tau_{zx} = \tau_{yz} = \tau_{zz}= 0 \end{align} $$

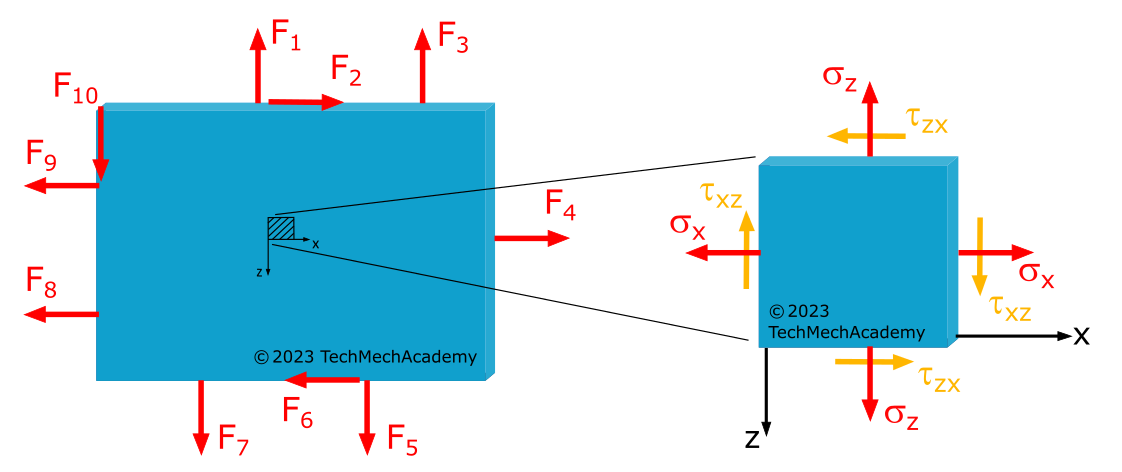
Natürlich könnte auch eine belastete $x$,$z$-Ebene vorliegen mit einer unbelasteten $y$-Achse oder eine belastete $y$,$z$-Ebene mit einer unbelasteten $z$-Achse. Die Orientierung des Koordinatensystems in der entsprechenden Ebene spielt dabei keine Rolle. Alle diese Fälle erfüllen eine der Bedingungen für das Vorliegen eines ebenen Spannungszustandes: Eine ebene Belastung mit lastfreier Oberfläche.

Eine weitere Bedingung für den ebenen Spannungszustand ist, dass die Dicke des Bauteils im Verhältnis zu seinen Längenabmessungen klein ist, also eine geringe Wandstärke vorhanden ist. Nur so können wir voraussetzen, dass die Spannungen $\sigma_x, \sigma_y$ und $\tau_{xy} = \tau_{yx}$ über die ganze Dicke der Scheibe gleichmäßig verteilt sind.

Nicht ganz klar, wo der Unterschied zwischen $\tau_{xy}$ und $\tau_{yx}$ bzw. $\tau_{xz}$ und $\tau_{zx}$ liegt? Schau bei der Indizierung der (Schub-)Spannungen nach.

Nicht ganz klar, warum $\tau_{xy} = \tau_{yx}$ bzw. $\tau_{xz} = \tau_{zx}$? Schau bei den zugeordneten Schubspannungen nach.

Nicht ganz klar, warum sich die Richtungen der Schubspannungen in den Abbildungen 1.3.1 und 1.3.2 unterscheiden? Schau bei der Vorzeichenfestlegung für Normal- und Schubspannungen nach.

3.1 Normal- und Schubspannungen unter einem beliebigen Schnittwinkel - Koordinatentransformation

Interessant sind für uns nicht nur die Normal- und Schubspannungen $\sigma_x, \sigma_y$ und $\tau_{xy} = \tau_{yx}$ (nach Abbildung 1.3.1) bzw. $\sigma_x, \sigma_z$ und $\tau_{xz} = \tau_{zx}$ (nach Abbildung 1.3.2) parallel zu den Koordinatenachsen, sondern vielmehr die Spannungen unter einem beliebigen Schnittwinkel $\varphi$.

Letztlich ist es wichtig zu wissen, unter welchem Schnittwinkel $\varphi$ die größten oder auch die kleinsten Spannungen im untersuchten Punkt des Bauteils wirken und wie groß diese sind. Nur so können beispielsweise die Winkel von notwendigen Schweißnähten sinnvoll gewählt werden, um die Belastungen dieser Nähte so gering wie möglich zu halten.

Wollen wir die Koordinatentransformation für den ebenen Spannungszustand herleiten, können wir dies für zwei verschiedene Koordinatensysteme tun: Einmal für ein kartesisches Koordinatensystem mit positiver x-Achse nach rechts und positiver y-Achse nach oben wie in Abbildung 1.3.1 gezeigt und einmal für ein kartesisches Koordinatensystem mit positiver x-Achse nach rechts und positiver z-Achse nach unten wie in Abbildung 1.3.2 gezeigt.

Wir müssen hier diese Unterscheidung vornehmen, weil die Richtung der Schubspannungen in der Ebene von der Wahl des Koordinatensystems abhängen. Dies liegt an der definierten Vorzeichenfestlegung für Normal- und Schubspannungen. In der Praxis reicht es aus, die Herleitung für ein bevorzugtes Koordinatensystem zu kennen und dessen Koordinatentransformation berechnen zu können. Da aber beide Systeme häufig verwendet werden, sollen an dieser Stelle beide Herleitungen gezeigt werden.

3.1.1 Koordinatentransformation für ein kartesisches Koordinatensystem mit positiver x-Achse nach rechts und positiver y-Achse nach oben

Es ist nicht das Koordinatensystem, das dich interessiert? Überspringe diesen Abschnitt! Weiter zu: 3.1.2 Koordinatentransformation für ein kartesisches Koordinatensystem mit positiver x-Achse nach rechts und positiver z-Achse nach unten

Um die Spannungen unter einem beliebigen Schnittwinkel zu definieren, führen wir wie beim einachsigen Spannungszustand ein um den (Schnitt-)Winkel $\varphi$ gedrehtes Koordinatensystem ein. Wir nennen die gedrehte $x$-Achse $\xi$ (Xi) und die gedrehte $y$-Achse $\eta$ (Eta).

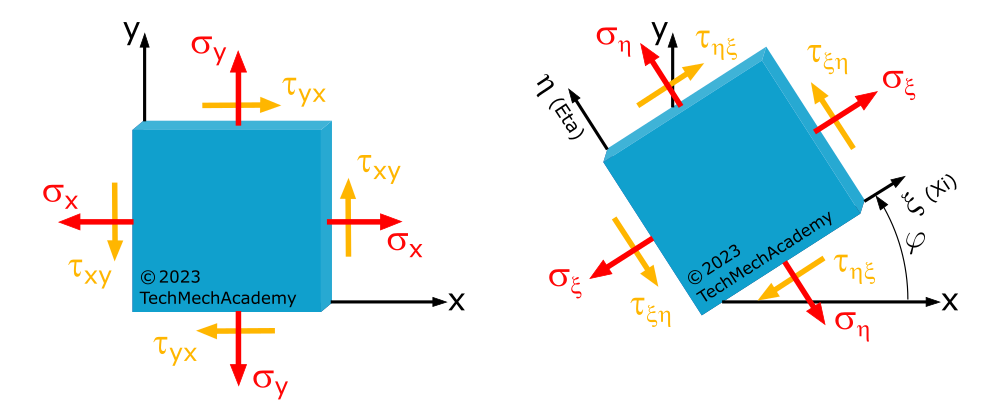
Diese Abbildung zeigt die Drehung des Koordinatensystems um den Schnittwinkel Phi. — Abb. 1.3.3: Drehung des Koordinatensystems

Wir erhalten die Normalspannungen $\sigma_{\xi}$, $\sigma_{\eta}$ und die Schubspannungen $\tau_{\xi\eta} = \tau_{\eta\xi}$.

Der Schnittwinkel $\varphi$ wird im $x$, $y$- Koordinatensystem am untersuchten Element gegen den Uhrzeigersinn positiv gezählt (vgl. Rechte-Hand-Regel im kartesischen Koordinatensystem + Rechte-Daumen-Regel zur Bestimmung der positiven Drehrichtung).

Um die beiden Koordinatensysteme aus Abbildung 1.3.3 mathematisch zu verknüpfen, schneiden wir das Flächenelement im $x$,$y$-Koordinatensystem im Winkel $\varphi$ und tragen die Spannungen an den Flächen an:

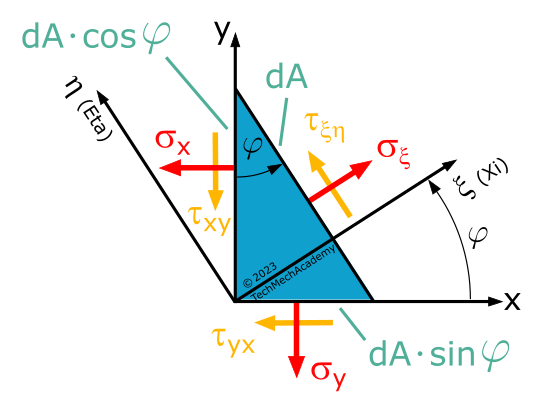
Diese Abbildung zeigt ein geschnittenes Volumenelement. — Abb. 1.3.4: Geschnittenes Volumenelement

Wir bilden jeweils das Kräftegleichgewicht in die $\xi$- und in die $\eta$-Richtung.

Beachte:

Da Gleichgewichtsaussagen nur für Kräfte gelten, müssen wir die Spannungen mit den Flächenelementen multiplizieren, in denen sie wirken!

$$ \definecolor{lsgreen}{RGB}{79,175,152} \definecolor{lsblue}{RGB}{16,160,205} \definecolor{lsyellow}{RGB}{255,182,0} \begin{align} \tag{2} \nearrow~:~ &\sigma_{\xi} \cdot {\color{lsgreen}\mathrm{d}A} - (\sigma_x \cdot {\color{lsgreen}\mathrm{d}A \cdot \cos(\varphi)}) \cdot \cos(\varphi) - (\sigma_y \cdot {\color{lsgreen}\mathrm{d}A \cdot \sin(\varphi)}) \cdot \sin(\varphi) - (\tau_{xy} \cdot {\color{lsgreen}\mathrm{d}A \cdot \cos(\varphi)}) \cdot \sin(\varphi) - (\tau_{yx} \cdot {\color{lsgreen}\mathrm{d}A \cdot \sin(\varphi)}) \cdot \cos(\varphi) = 0\\[10pt] \tag{3} \nwarrow~:~ &\tau_{\xi\eta} \cdot {\color{lsgreen}\mathrm{d}A} + (\sigma_x \cdot {\color{lsgreen}\mathrm{d}A \cdot \cos(\varphi)}) \cdot \sin(\varphi) - (\sigma_y \cdot {\color{lsgreen}\mathrm{d}A \cdot \sin(\varphi)}) \cdot \cos(\varphi) - (\tau_{xy} \cdot {\color{lsgreen}\mathrm{d}A \cdot \cos(\varphi)}) \cdot \cos(\varphi) + (\tau_{yx} \cdot {\color{lsgreen}\mathrm{d}A \cdot \sin(\varphi)}) \cdot \sin(\varphi) = 0 \end{align} $$

Wir können aus beiden Gleichungen (2) und (3) jeweils $\mathrm{d}A$ ausklammern und eliminieren.

Mit $\tau_{yx} = \tau_{xy}$ erhalten wir dann:

$$ \begin{align} \tag{4} \sigma_{\xi} &= \sigma_x \cdot \cos(\varphi) \cdot \cos(\varphi) + \sigma_y \cdot \sin(\varphi) \cdot \sin(\varphi) + \tau_{xy} \cdot \cos(\varphi) \cdot \sin(\varphi) + \tau_{xy} \cdot \sin(\varphi) \cdot \cos(\varphi)\\ \tag{5} \tau_{\xi\eta} &= - \sigma_x \cdot \cos(\varphi) \cdot \sin(\varphi) + \sigma_y \cdot \sin(\varphi) \cdot \cos(\varphi) + \tau_{xy} \cdot \cos(\varphi) \cdot \cos(\varphi) - \tau_{xy} \cdot \sin(\varphi) \cdot \sin(\varphi) \end{align} $$

Zusammengefasst ergibt das:

$$ \begin{align} \tag{6} \sigma_{\xi} &= \sigma_x \cdot \cos^2(\varphi) + \sigma_y \cdot \sin^2(\varphi) + 2 \cdot \tau_{xy} \cdot \sin(\varphi) \cdot \cos(\varphi) \\ \tag{7} \tau_{\xi\eta} &= - (\sigma_x - \sigma_y) \cdot \sin(\varphi) \cdot \cos(\varphi) + \tau_{xy} \cdot (\cos^2(\varphi) - \sin^2(\varphi)) \end{align} $$

Jetzt fehlt noch eine Formel für die Normalspannung $\sigma_{\eta}$. Diese Normalspannung wirkt in einem Winkel von 90° (oder auch $\frac{\pi}{2}$) zur Normalspannung $\sigma_{\xi}$.

Also können wir die ermittelte Formel für die Normalspannung $\sigma_{\xi}$ verwenden und $\sigma_{\xi}$ durch $\sigma_{\eta}$ sowie $\varphi$ durch $\varphi + \frac{\pi}{2}$ ersetzen:

$$ \begin{align} \tag{8} \sigma_{\eta} &= \sigma_x \cdot \cos^2\Bigl(\varphi+\frac{\pi}{2}\Bigr) + \sigma_y \cdot \sin^2\Bigl(\varphi+\frac{\pi}{2}\Bigr) + 2 \cdot \tau_{xy} \cdot \sin\Bigl(\varphi+\frac{\pi}{2}\Bigr) \cdot \cos\Bigl(\varphi+\frac{\pi}{2}\Bigr) \end{align} $$

Mithilfe der trigonometrischen Additionstheoreme

$$ \begin{align} \tag{9} \sin\Bigl(\varphi + \frac{\pi}{2}\Bigr) = \sin (\varphi) \cdot \cos\Bigl(\frac{\pi}{2}\Bigr) +\cos (\varphi) \cdot \sin\Bigl(\frac{\pi}{2}\Bigr) \end{align} $$

und

$$ \begin{align} \tag{10} \cos\Bigl(\varphi + \frac{\pi}{2}\Bigr) = \cos (\varphi) \cdot \cos\Bigl(\frac{\pi}{2}\Bigr) - \sin (\varphi) \cdot \sin\Bigl(\frac{\pi}{2}\Bigr) \end{align} $$

und nach Einsetzen der Funktionswerte

$$ \begin{align} \tag{11} &\sin\Bigl(\frac{\pi}{2}\Bigr) = 1\\[10pt] \tag{12} &\cos\Bigl(\frac{\pi}{2}\Bigr) = 0\\[10pt] \tag{13} \Rightarrow \qquad &\sin\Bigl(\varphi + \frac{\pi}{2}\Bigr) = \sin(\varphi) \cdot 0 + \cos (\varphi) \cdot 1 = +\cos (\varphi)\\[10pt] \tag{14} &\cos\Bigl(\varphi + \frac{\pi}{2}\Bigr) = \cos(\varphi) \cdot 0 - \sin (\varphi) \cdot 1 = - \sin (\varphi) \end{align} $$

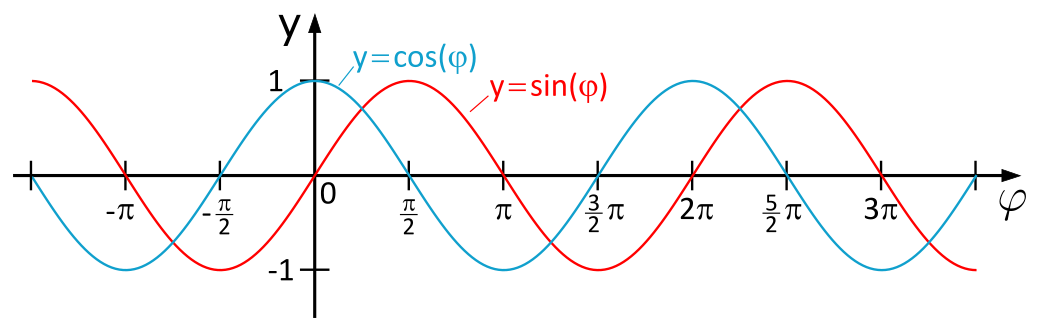
Diese Abbildung zeigt die Sinus- und Kosinunsfunktionen. — Abb. 1.3.5: Sinus- und Kosinusfunktion

erhalten wir:

$$ \begin{align} \tag{15} \sigma_{\eta} &= \sigma_x \cdot \sin^2(\varphi) + \sigma_y \cdot \cos^2(\varphi) - 2 \cdot \tau_{xy} \cdot \sin(\varphi) \cdot \cos(\varphi) \end{align} $$

Zusammenfassend haben wir somit die Spannungen, die bei einem beliebigen Schnittwinkel auftreten, wie folgt ermittelt:

$$ \begin{align} \tag{16} \sigma_{\xi} &= \sigma_x \cdot \cos^2(\varphi) + \sigma_y \cdot \sin^2(\varphi) + 2 \cdot \tau_{xy} \cdot \sin(\varphi) \cdot \cos(\varphi) \\[7pt] \tag{17} \sigma_{\eta} &= \sigma_x \cdot \sin^2(\varphi) + \sigma_y \cdot \cos^2(\varphi) - 2 \cdot \tau_{xy} \cdot \sin(\varphi) \cdot \cos(\varphi) \\[7pt] \tag{18} \tau_{\xi\eta} &= - (\sigma_x - \sigma_y) \cdot \sin(\varphi) \cdot \cos(\varphi) + \tau_{xy} \cdot (\cos^2(\varphi) - \sin^2(\varphi)) \end{align} $$

Mit den trigonometrischen Formeln für Potenzen

$$ \begin{align} \tag{19} \sin^2(\varphi) &= \dfrac{1}{2}\bigl(1-\cos(2\varphi)\bigr)\\[7pt] \tag{20} \cos^2(\varphi) &= \dfrac{1}{2}\bigl(1+\cos(2\varphi)\bigr) \end{align} $$

und den Formeln für doppelte Winkel

$$ \begin{align} \tag{21} \sin(2\varphi) &= 2 \cdot \sin(\varphi) \cdot \cos(\varphi)\\[7pt] \tag{22} \cos(2\varphi) &= \cos^2(\varphi) - \sin^2(\varphi) \end{align} $$

erhalten wir die Transformationsgleichungen für den ebenen Spannungszustand:

$$ \begin{alignat}{3} \sigma_{\xi} &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) &&+ \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \cos(2\varphi) + \tau_{xy} \cdot \sin(2\varphi) \\[10pt] \sigma_{\eta} &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_y\Bigr) &&- \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \cos(2\varphi) - \tau_{xy} \cdot \sin(2\varphi) \\[10pt] \tau_{\xi\eta} &= &&- \dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_y\Bigr) \cdot \sin(2\varphi) + \tau_{xy} \cdot \cos(2\varphi) \end{alignat} $$

(1.7_xy)

Sind uns also die Normalspannungen $\sigma_x$ und $\sigma_y$ sowie die Schubspannungen $\tau_{xy}=\tau_{yx}$ für einen senkrechten Schnitt bekannt, dann können wir mithilfe der Transformationsgleichungen die Normalspannungen $\sigma_{\xi}$ und $\sigma_{\eta}$ sowie die Schubspannungen $\tau_{\xi\eta}=\tau_{\eta\xi}$ für einen beliebigen Schnittwinkel $\varphi$ berechnen.

Hinweis:

Obwohl es sich um zwei zueinander verdrehte Koordinatensysteme handelt, bleibt der Spannungszustand für den untersuchten Punkt im Bauteil gleich. Der Spannungszustand ist also unabhängig von der Änderung des Schnittwinkels $\varphi$. Die Zahlenwerte des Spannungszustandes hängen jedoch von dem Schnittwinkel $\varphi$ ab. Wir ändern folglich lediglich den Blickwinkel auf den Spannungszustand.

Interessant: Wir können aus der Gleichung (1.7_xy) die Gleichungen (1.4) und (1.5_xy) für den einachsigen Spannungszustand herleiten, denn beim einachsigen Spannungszustand gilt $\sigma_y = \tau_{xy}=0$:

$$ \begin{align} \tag{23} \sigma_{\xi} &= \dfrac{1}{2} \cdot \sigma_x + \dfrac{1}{2} \cdot \sigma_x \cdot \cos(2\varphi) = \dfrac{\sigma_x}{2}\bigl(1+\cos(2\varphi)\bigr)\\[10pt] \tag{24} \tau_{\xi\eta} &= - \dfrac{1}{2} \cdot \sigma_x \cdot \sin(2\varphi) = - \dfrac{\sigma_x}{2}\bigl(\sin(2\varphi)\bigr) \end{align} $$

3.1.2 Koordinatentransformation für ein kartesisches Koordinatensystem mit positiver x-Achse nach rechts und positiver z-Achse nach unten

Es ist nicht das Koordinatensystem, das dich interessiert? Überspringe diesen Abschnitt! Weiter zu: 3.1.3 Summe der Normalspannungen unter beliebigem Schnittwinkel

Um die Spannungen unter einem beliebigen Schnittwinkel zu definieren, führen wir wie beim einachsigen Spannungszustand ein um den (Schnitt-)Winkel $\varphi$ gedrehtes Koordinatensystem ein. Wir nennen die gedrehte $x$-Achse $\xi$ (Xi) und die gedrehte $z$-Achse $\eta$ (Eta).

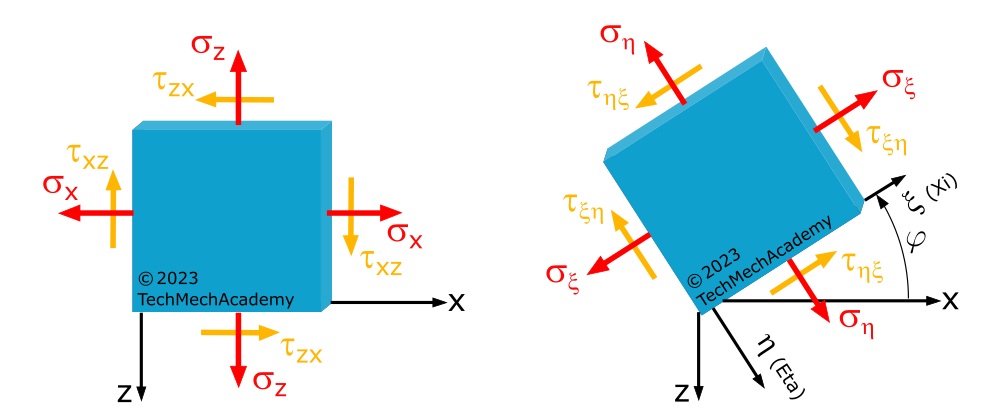
Wir erhalten die Normalspannungen $\sigma_{\xi}$, $\sigma_{\eta}$ und die Schubspannungen $\tau_{\xi\eta} = \tau_{\eta\xi}$.

Der Schnittwinkel $\varphi$ wird im $x$, $z$- Koordinatensystem am untersuchten Element gegen den Uhrzeigersinn positiv gezählt (vgl. Rechte-Hand-Regel im kartesischen Koordinatensystem + Rechte-Daumen-Regel zur Bestimmung der positiven Drehrichtung).

Um die beiden Koordinatensysteme aus Abbildung 1.3.6 mathematisch zu verknüpfen, schneiden wir das Flächenelement im $x$,$z$-Koordinatensystem im Winkel $\varphi$ und tragen die Spannungen an den Flächen an:

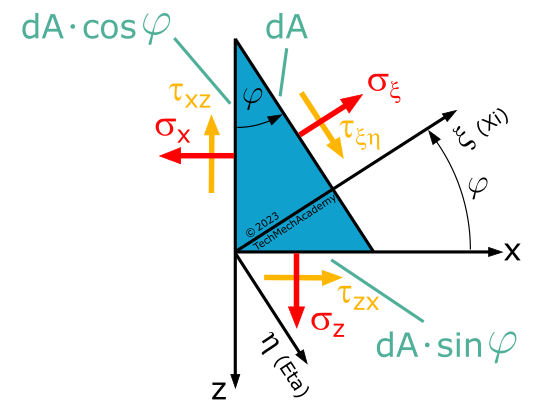
Wir bilden jeweils das Kräftegleichgewicht in die $\xi$- und in die $\eta$-Richtung.

Beachte:

Da Gleichgewichtsaussagen nur für Kräfte gelten, müssen wir die Spannungen mit den Flächenelementen multiplizieren, in denen sie wirken!

$$ \definecolor{lsgreen}{RGB}{79,175,152} \definecolor{lsblue}{RGB}{16,160,205} \definecolor{lsyellow}{RGB}{255,182,0} \begin{align} \tag{25} \nearrow~:~ &\sigma_{\xi} \cdot {\color{lsgreen}\mathrm{d}A} - (\sigma_x \cdot {\color{lsgreen}\mathrm{d}A \cdot \cos(\varphi)}) \cdot \cos(\varphi) - (\sigma_z \cdot {\color{lsgreen}\mathrm{d}A \cdot \sin(\varphi)}) \cdot \sin(\varphi) + (\tau_{xz} \cdot {\color{lsgreen}\mathrm{d}A \cdot \cos(\varphi)}) \cdot \sin(\varphi) + (\tau_{zx} \cdot {\color{lsgreen}\mathrm{d}A \cdot \sin(\varphi)}) \cdot \cos(\varphi) = 0\\[10pt] \tag{26} \searrow~:~ &\tau_{\xi\eta} \cdot {\color{lsgreen}\mathrm{d}A} - (\sigma_x \cdot {\color{lsgreen}\mathrm{d}A \cdot \cos(\varphi)}) \cdot \sin(\varphi) + (\sigma_z \cdot {\color{lsgreen}\mathrm{d}A \cdot \sin(\varphi)}) \cdot \cos(\varphi) - (\tau_{xz} \cdot {\color{lsgreen}\mathrm{d}A \cdot \cos(\varphi)}) \cdot \cos(\varphi) + (\tau_{zx} \cdot {\color{lsgreen}\mathrm{d}A \cdot \sin(\varphi)}) \cdot \sin(\varphi) = 0 \end{align} $$

Wir können aus beiden Gleichungen (25) und (26) jeweils $\mathrm{d}A$ ausklammern und eliminieren.

Mit $\tau_{zx} = \tau_{xz}$ erhalten wir dann:

$$ \begin{align} \tag{27} \sigma_{\xi} &= \sigma_x \cdot \cos(\varphi) \cdot \cos(\varphi) + \sigma_z \cdot \sin(\varphi) \cdot \sin(\varphi) - \tau_{xz} \cdot \cos(\varphi) \cdot \sin(\varphi) - \tau_{xz} \cdot \sin(\varphi) \cdot \cos(\varphi)\\ \tag{28} \tau_{\xi\eta} &= \sigma_x \cdot \cos(\varphi) \cdot \sin(\varphi) - \sigma_z \cdot \sin(\varphi) \cdot \cos(\varphi) + \tau_{xz} \cdot \cos(\varphi) \cdot \cos(\varphi) - \tau_{xz} \cdot \sin(\varphi) \cdot \sin(\varphi) \end{align} $$

Zusammengefasst ergibt das:

$$ \begin{align} \tag{29} \sigma_{\xi} &= \sigma_x \cdot \cos^2(\varphi) + \sigma_z \cdot \sin^2(\varphi) - 2 \cdot \tau_{xz} \cdot \sin(\varphi) \cdot \cos(\varphi) \\ \tag{30} \tau_{\xi\eta} &= (\sigma_x - \sigma_z) \cdot \sin(\varphi) \cdot \cos(\varphi) + \tau_{xz} \cdot (\cos^2(\varphi) - \sin^2(\varphi)) \end{align} $$

Jetzt fehlt noch eine Formel für die Normalspannung $\sigma_{\eta}$. Diese Normalspannung wirkt in einem Winkel von -90° (oder auch $-\frac{\pi}{2}$) zur Normalspannung $\sigma_{\xi}$.

Also können wir die ermittelte Formel für die Normalspannung $\sigma_{\xi}$ verwenden und $\sigma_{\xi}$ durch $\sigma_{\eta}$ sowie $\varphi$ durch $\varphi - \frac{\pi}{2}$ ersetzen:

$$ \begin{align} \tag{31} \sigma_{\eta} &= \sigma_x \cdot \cos^2\Bigl(\varphi-\frac{\pi}{2}\Bigr) + \sigma_z \cdot \sin^2\Bigl(\varphi-\frac{\pi}{2}\Bigr) - 2 \cdot \tau_{xz} \cdot \sin\Bigl(\varphi-\frac{\pi}{2}\Bigr) \cdot \cos\Bigl(\varphi-\frac{\pi}{2}\Bigr) \end{align} $$

Mithilfe der trigonometrischen Additionstheoreme

$$ \begin{align} \tag{32} \sin\Bigl(\varphi - \frac{\pi}{2}\Bigr) = \sin (\varphi) \cdot \cos\Bigl(\frac{\pi}{2}\Bigr) -\cos (\varphi) \cdot \sin\Bigl(\frac{\pi}{2}\Bigr) \end{align} $$

und

$$ \begin{align} \tag{33} \cos\Bigl(\varphi - \frac{\pi}{2}\Bigr) = \cos (\varphi) \cdot \cos\Bigl(\frac{\pi}{2}\Bigr) + \sin (\varphi) \cdot \sin\Bigl(\frac{\pi}{2}\Bigr) \end{align} $$

und nach Einsetzen der Funktionswerte

$$ \begin{align} \tag{34} &\sin\Bigl(\frac{\pi}{2}\Bigr) = 1\\[10pt] \tag{35} &\cos\Bigl(\frac{\pi}{2}\Bigr) = 0\\[10pt] \tag{36} \Rightarrow \qquad &\sin\Bigl(\varphi - \frac{\pi}{2}\Bigr) = \sin(\varphi) \cdot 0 - \cos (\varphi) \cdot 1 = -\cos (\varphi)\\[10pt] \tag{37} &\cos\Bigl(\varphi - \frac{\pi}{2}\Bigr) = \cos(\varphi) \cdot 0 + \sin (\varphi) \cdot 1 = +\sin (\varphi) \end{align} $$

erhalten wir:

$$ \begin{align} \tag{38} \sigma_{\eta} &= \sigma_x \cdot \sin^2(\varphi) + \sigma_z \cdot \cos^2(\varphi) + 2 \cdot \tau_{xz} \cdot \sin(\varphi) \cdot \cos(\varphi) \end{align} $$

Zusammenfassend haben wir somit die Spannungen, die bei einem beliebigen Schnittwinkel auftreten, wie folgt ermittelt:

$$ \begin{align} \tag{39} \sigma_{\xi} &= \sigma_x \cdot \cos^2(\varphi) + \sigma_z \cdot \sin^2(\varphi) - 2 \cdot \tau_{xz} \cdot \sin(\varphi) \cdot \cos(\varphi) \\[7pt] \tag{40} \sigma_{\eta} &= \sigma_x \cdot \sin^2(\varphi) + \sigma_z \cdot \cos^2(\varphi) + 2 \cdot \tau_{xz} \cdot \sin(\varphi) \cdot \cos(\varphi) \\[7pt] \tag{41} \tau_{\xi\eta} &= (\sigma_x - \sigma_z) \cdot \sin(\varphi) \cdot \cos(\varphi) + \tau_{xz} \cdot (\cos^2(\varphi) - \sin^2(\varphi)) \end{align} $$

Mit den trigonometrischen Formeln für Potenzen

$$ \begin{align} \tag{42} \sin^2(\varphi) &= \dfrac{1}{2}\bigl(1-\cos(2\varphi)\bigr)\\[7pt] \tag{43} \cos^2(\varphi) &= \dfrac{1}{2}\bigl(1+\cos(2\varphi)\bigr) \end{align} $$

und den Formeln für doppelte Winkel

$$ \begin{align} \tag{44} \sin(2\varphi) &= 2 \cdot \sin(\varphi) \cdot \cos(\varphi)\\[7pt] \tag{45} \cos(2\varphi) &= \cos^2(\varphi) - \sin^2(\varphi) \end{align} $$

erhalten wir die Transformationsgleichungen für den ebenen Spannungszustand:

$$ \begin{alignat}{3} \sigma_{\xi} &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) + &&\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \cos(2\varphi) - \tau_{xz} \cdot \sin(2\varphi) \\[10pt] \sigma_{\eta} &= \dfrac{1}{2} \cdot \Bigl(\sigma_x + \sigma_z\Bigr) - &&\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \cos(2\varphi) + \tau_{xz} \cdot \sin(2\varphi) \\[10pt] \tau_{\xi\eta} &= &&\dfrac{1}{2} \cdot \Bigl(\sigma_x - \sigma_z\Bigr) \cdot \sin(2\varphi) + \tau_{xz} \cdot \cos(2\varphi) \end{alignat} $$

(1.7_xz)

Sind uns also die Normalspannungen $\sigma_x$ und $\sigma_z$ sowie die Schubspannungen $\tau_{xz}=\tau_{zx}$ für einen senkrechten Schnitt bekannt, dann können wir mithilfe der Transformationsgleichungen die Normalspannungen $\sigma_{\xi}$ und $\sigma_{\eta}$ sowie die Schubspannungen $\tau_{\xi\eta}=\tau_{\eta\xi}$ für einen beliebigen Schnittwinkel $\varphi$ berechnen.

Hinweis:

Obwohl es sich um zwei zueinander verdrehte Koordinatensysteme handelt, bleibt der Spannungszustand für den untersuchten Punkt im Bauteil gleich. Der Spannungszustand ist also unabhängig von der Änderung des Schnittwinkels $\varphi$. Die Zahlenwerte des Spannungszustandes hängen jedoch von dem Schnittwinkel $\varphi$ ab. Wir ändern folglich lediglich den Blickwinkel auf den Spannungszustand.

Interessant: Wir können aus der Gleichung (1.7_xz) die Gleichungen (1.4) und (1.5_xz) für den einachsigen Spannungszustand herleiten, denn beim einachsigen Spannungszustand gilt $\sigma_z = \tau_{xz}=0$:

$$ \begin{align} \tag{46} \sigma_{\xi} &= \dfrac{1}{2} \cdot \sigma_x + \dfrac{1}{2} \cdot \sigma_x \cdot \cos(2\varphi) = \dfrac{\sigma_x}{2}\bigl(1+\cos(2\varphi)\bigr)\\[10pt] \tag{47} \tau_{\xi\eta} &= \dfrac{1}{2} \cdot \sigma_x \cdot \sin(2\varphi) = \dfrac{\sigma_x}{2}\bigl(\sin(2\varphi)\bigr) \end{align} $$

3.1.3 Summe der Normalspannungen unter beliebigem Schnittwinkel

Addieren wir die ersten beiden Gleichungen aus (1.7_xy) oder (1.7_xz), erhalten wir die Erkenntnis, dass die Summe der Normalspannungen für einen Punkt in einer Ebene im Bauteil unter jedem beliebigen Schnittwinkel $\varphi$ immer gleich ist:

$$ \begin{aligned} \sigma_x + \sigma_y = \sigma_{\xi} + \sigma_{\eta} = \text{konst.} \end{aligned} $$

(1.8)

Festigkeitslehre / Elastostatik

Thema: Spannungszustand

3. Ebener Spannungszustand

3.1 Normal- und Schubspannungen unter einem beliebigen Schnittwinkel - Koordinatentransformation

3.1.1 Koordinatentransformation für ein kartesisches Koordinatensystem mit positiver x-Achse nach rechts und positiver y-Achse nach oben

Beachte:

Hinweis:

3.1.2 Koordinatentransformation für ein kartesisches Koordinatensystem mit positiver x-Achse nach rechts und positiver z-Achse nach unten

Beachte:

Hinweis:

3.1.3 Summe der Normalspannungen unter beliebigem Schnittwinkel

Mehr erfahren?

Passende Übungsaufgaben: