2. Erste Grundaufgabe: Reduktion auf eine Einzelkraft
Okay, Ingenieur*in in spe, aufgepasst! Hier geht es um die erste Grundaufgabe der Statik für zentrale Kräftesysteme: die Reduktion eines Kräftesystems auf eine Einzelkraft. Klingt kompliziert? Ist es aber nicht! Mit ein bisschen Zeichentalent und unserem schlauen Freund, dem Kräfteparallelogramm, lösen wir das Problem im Handumdrehen.
Also, schnapp dir deinen Bleistift, Lineal und deinen besten Kumpel, den Taschenrechner, und los geht's!
Stellen wir uns vor: Ein starrer Körper, bedrängt von drei fiesen Kräften F1, F2 und F3. Sie zerren, drücken und ziehen an ihm herum, wie wildgewordene Ameisen an einem Bonbon. Aber wir lassen uns nicht einschüchtern! Mit unserem genialen Wissen und ein paar geschickten Zeichnungen bändigen wir diese Biester im Handumdrehen.
Unser Ziel: Wir bestimme die Resultierende dieser drei Kräfte. Die Resultierende ist eine Einzelkraft, die den gleichen Effekt hat wie die drei Einzelkräfte zusammen.
Was ist ein Lageplan? Der Lageplan ist eine maßstäbliche Zeichnung, die die geometrische Anordnung aller relevanten Elemente eines Systems zeigt. Dazu gehören:
- Körper: Die zu untersuchenden starren Körper oder Bauteile.
- Lager: Die Punkte, an denen der Körper mit seiner Umgebung verbunden ist.
- Kräfte: Die auf den Körper wirkenden Kräfte und Momente.
- Weitere Elemente: Abmessungen, Koordinatensysteme, etc.
Warum ist der Lageplan ein wichtiges Werkzeug zur Lösung von Aufgaben der Technischen Mechanik?
Der Lageplan:
- Verdeutlicht die geometrische Anordnung des Systems.
- Ermöglicht die Bestimmung von Winkeln und Längen.
- Ist Grundlage für die Erstellung des Kräfteplans
Stellen wir uns einfach vor, unsere Aufgabenstellung hätte den folgenden Lageplan gegeben:
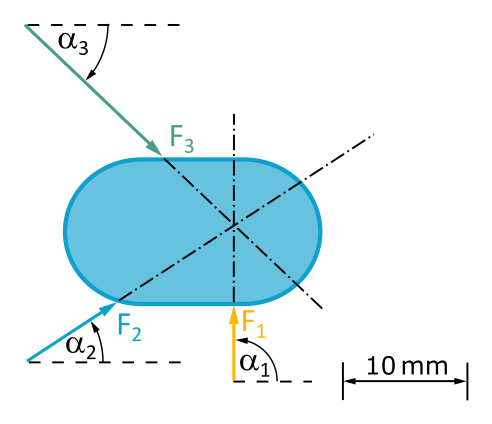
Die Wirkungslinien der Kräfte schneiden sich in einem Punkt. Es liegt also ein zentrales Kräftesystem vor.
Was ist ein Kräfteplan? Der Kräfteplan dient dazu, die an einem Objekt wirkenden Kräfte grafisch darzustellen und zu analysieren. In diesem Plan werden die einzelnen Kräfte, die auf das Tragwerk wirken, als Pfeile (Vektoren) eingezeichnet. Die Pfeillänge entspricht dabei dem Betrag der Kraft und die Pfeilrichtung ihrer Wirkrichtung. Entsprechend ist der Maßstab eines Kräfteplans Kraft pro Längeneinheit.
Erinnerung: Das Kräfteparallelogramm ist ein cleveres Werkzeug, um zwei Kräfte zu einer einzigen Kraft zusammenzufassen.
- Zunächst wählen wir im Kräfteplan einen beliebigen Startpunkt S.
- Nun wählen wir zwei beliebige Kräfte aus dem Lageplan (z.B. F1 und F2).
-
Wir zeichnen das Kräfteparallelogramm für diese beiden Kräfte. Die nötigen Winkel können wir im Lageplan ablesen.
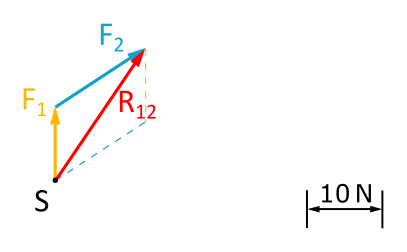
Abb. 3.2.2: Kräfteparallelogramm -
Wir bilden das Kräfteparallelogramm für die Resultierende des vorherigen Kräfteparallelogramms und einer beliebigen weitern Kraft, die wir bisher noch nicht eingezeichnet haben.
In diesem Fall bleibt nur F3 übrig.
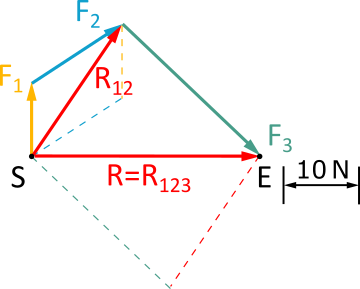
Abb. 3.2.3: Kräfteparallelogramm aus allen drei Kräften - Die Resultierende des letzten Kräfteparallelogramms ist die Gesamtresultierende.
- Wähle einen Startpunkt S.
- Zeichne alle Kraftvektoren maßstabsgetreu ein. Beginne mit einem beliebigen Kraftvektor am Startpunkt S.
- Zeichne nach und nach die anderen Kraftvektoren in beliebiger Reihenfolge ein. Jeder Vektor beginnt an der Pfeilspitze seines Vorgängers.
- An der Pfeilspitze des zuletzt eingezeichneten Kraftvektors liegt der Endpunkt E (vgl. Abb. 3.2.3)
- Die Resultierende R ist die Verbindungslinie vom Startpunkt S zum Endpunkt E. Das bedeutet, ihre Richtung ist dem Umlaufsinn des offenen Kräftepolygons (S nach E) entgegengesetzt.
- Durch Messen der Länge der Resultierenden erhalten wir unter Beachtung des verwendeten Maßstabes den Betrag der Resultierenden.
- Auch den Richtungswinkel der Resultierenden können wir ausmessen.
Bleibt noch eine Frage: Wo liegt die Wirkungslinie der Resultierenden im Lageplan?
Klar: Da alle Kräfte im zentralen Kräftesystem durch einen Punkt verlaufen, muss auch die Wirkungslinie der Resultierenden durch diesen Punkt verlaufen:
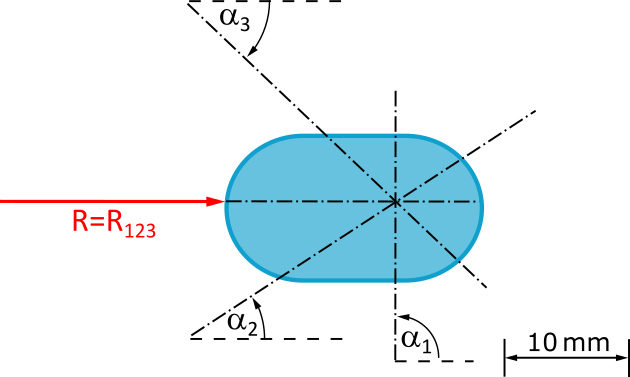
Doch wo genau auf dieser Wirkungslinie greift die resultierende Kraft an? Wird unser Bonbon geschoben oder gezogen? Der Verschiebungssatz gibt die Antwort: Wir können darüber keine Aussage treffen, es spielt für die Wirkung der Kraft auf den starren Körper aber auch keine Rolle.
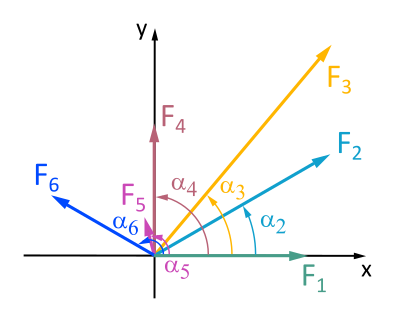
Ermittle grafisch und analytisch aus den Kräften F1 bis F6 den Betrag und die Richtung für die Resultierende.
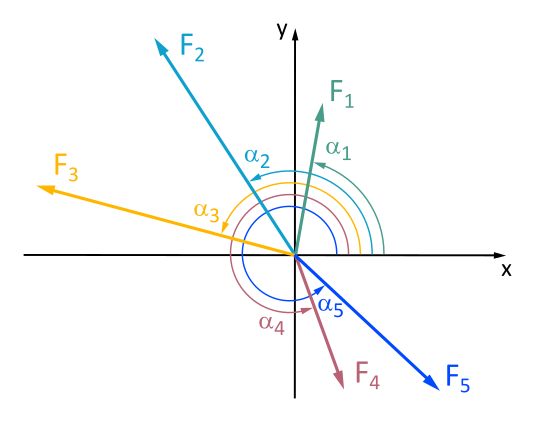
Ermittle grafisch und analytisch aus den Kräften F1 bis F5 den Betrag und die Richtung für die Resultierende.
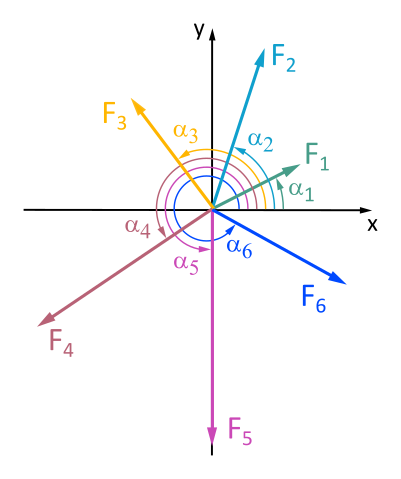
Ermittle grafisch und analytisch aus den Kräften F1 bis F6 den Betrag und die Richtung für die Resultierende.