2.1 Normalspannung bei einachsiger Beanspruchung
Okay, genug von der formellen Einleitung. Kommen wir zum spannenden Teil. Heute tauchen wir ein in die spannende Welt der einachsigen Beanspruchung. Klingt kompliziert? Ist es aber nicht! Stell dir einfach einen Stab vor, der von einer fiesen Kraft entweder gezogen oder gedrückt wird. So einfach ist das!
Na klar, der arme Stab wird verformt. Und genau diese Verformung interessiert uns. Denn sie verrät uns, wie viel Spannung im Material steckt.

Normalspannung heißt das Zauberwort. Sie beschreibt die Kraft, die pro Fläche auf den armen Stab wirkt. Ist die Kraft positiv, also zieht der Stab, sprechen wir von Zugspannung. Drückt die Kraft hingegen, wird's zur Druckspannung – negativ, aber hey, Spannung ist Spannung!
Bei einachsiger Beanspruchung und gleichmäßiger Verteilung der inneren Kräfte gilt für eine Schnittfläche senkrecht zur Stabsachse:
(1.3)
F ist die Kraft, A die Querschnittsfläche. Merk dir einfach: Spannung ist Kraft pro Fläche, easy peasy!
| Zeichen | Name | Größe | Einheit |
|---|---|---|---|
| \(\sigma_x\) | Sigma | Normalspannung in x-Richtung | N/mm2 = MPa |
| \(N_x\) | Normalkraft in x-Richtung | N | |
| \(F\) | Außen angreifende Zug- oder Druckkraft | N | |
| \(A\) | Fläche | mm2 |
- Die Kraft muss senkrecht zur Fläche wirken.
- Die Fläche muss die Querschnittsfläche des Stabes sein.
Klaro! Stell dir einen 10 cm2 großen Stab vor, der mit 100 N belastet wird.
Auf jeden Quadratzentimeter des Stabes wirken 10 N Kraft. Ganz schön viel, oder?
Die Schubspannung spielt bei der einachsigen Beanspruchung keine Rolle. Da der Spannungsvektor \(\vec{t}\) in diesem Fall senkrecht auf der Fläche steht, entfällt die Komponente Schubspannung, d.h. \(\tau=0\). Es gilt damit wegen der Richtung von \(\vec{t}\) in Richtung der Flächennormalen \(\vec{\sigma} = \vec{t}\)!
Also ist die Schubspannung nur bei schrägen Belastungen relevant. Aber keine Sorge, auch die kriegen wir irgendwann hin!
Okay, okay, es geht noch spannender! Was passiert, wenn die Kraft oder die Querschnittsfläche nicht konstant sind?
Dann ist die Spannung auch nicht konstant. Zum Beispiel bei einem hängenden Kegel.

Wo ist die Spannung im abgebildeten hängenden Kreiskegel am kleinsten:
- Unten an der Spitze
- Oben an der größten Kreisfläche
- Weder noch
Die richtige Antwort ist natürlich 1. Die Spannung ist unten an der Spitze des Kreiskegels am kleinsten.
Liegt es daran, dass der Querschnitt des Kreiskegels, also die Fläche A(x) hier am kleinsten ist?
Nein, das ist nicht die Ursache. Da wir keine äußere Krafteinwirkung haben, wirkt hier die kleinste bzw. gar keine Gewichtkraft. Denn der Kreiskegel ist oben aufgehängt, hier zieht seine gesamte Gewichtskraft an der Querschnittsfläche. Je weiter wir zur Spitze wandern, desto kleiner auch die ziehende Gewichtskraft. Und wo keine Kraft ist, kann natürlich auch keine Spannung sein!
Bei unserem Kreiskegel ist es so, dass die Normalkraft aufgrund der veränderlichen Gewichtskraft bei verschiedenen Schnitten ebenso wie der Durchmesser von x abhängen. Dann hängt auch die Spannung von x ab, d.h. sie ist an jeder Stelle x unterschiedlich:
(1.3b)
Einachsige Beanspruchung ist easy peasy! Mit ein bisschen Formelkram und Fantasie kannst du die Spannung in jedem Material berechnen.
Studiere das folgende Beispiel und teste dein Wissen! Berechne die Spannung in einem Stab deiner Wahl. Viel Spaß!
Beispiel 1.1: Konischer Stab
Ein konischer Stab mit kreisförmigem Querschnitt und der Länge \(l = 250~\mathrm{mm}\) wird wie in Abbildung B1 dargestellt durch eine Druckkraft \(F=10~\mathrm{kN}\) in der Stabsachse belastet. Der Durchmesser bei \(x=0\) sei mit \(2d_0 = 150~\mathrm{mm}\) doppelt so groß wie der Durchmesser bei \(x=l\) mit \(d_0 = 75~\mathrm{mm}\).
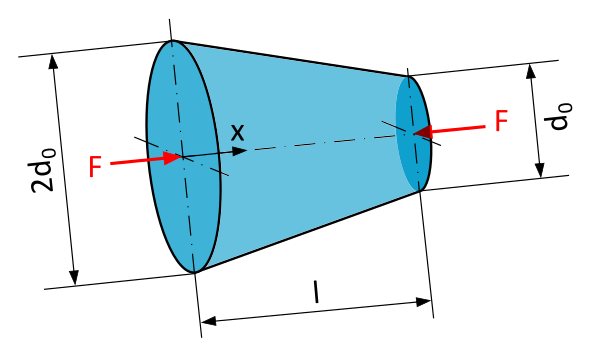
- Wie lautet die Formel zur Berechnung der Normalspannung \(\sigma\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Stabsachse?
- Wie groß ist die Normalspannung \(\sigma\) an der Stelle \(x=200~\mathrm{mm}\) in einem Schnitt senkrecht zur Stabsachse?
Lösung
Vorüberlegungen
Der Stab wird durch eine Kraft \(F\) belastet, deren Wirkungslinie die Stabsachse ist. Das bedeutet: Es liegt ein einachsiger Spannungszustand vor.
Wir suchen die Normalspannung in einem senkrechten Schnitt zur Stabsachse. Die allgemeine Formel lautet:
(1.3)
Der Schwierigkeitsgrad dieser Aufgabe besteht darin, dass die Querschnittsfläche \(A\) des Stabes konisch und damit für jede Position \(x\) unterschiedlich ist. Also gilt \(A=A(x)\). Wir benötigen entsprechend die Formel 1.3b, um diese Aufgabe zu lösen:
(1.3b)
- Wie lautet die Formel zur Berechnung der Normalspannung \(\sigma\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Stabsachse?
Schritt 1: Normalkraft bestimmen
Stelle dir vor, du schneidest den Stab an einem beliebigen Punkt \(x\) gedanklich durch. An der Schnittstelle wirken zwei Kräfte, entgegengesetzt und gleich groß: die Normalkraft N in doppelter Ausführung. Denn nur so kann diese Schnittstelle im Gleichgewicht sein.
Zur Erinnerung: Am positiven, linken Schnittufer tragen wir \(N\) in positiver (in Richtung der positiven x-Achse) Richtung an, am negativen, rechten Schnittufer hingegen in negativer (gegen die Richtung der positiven x-Achse) Richtung.
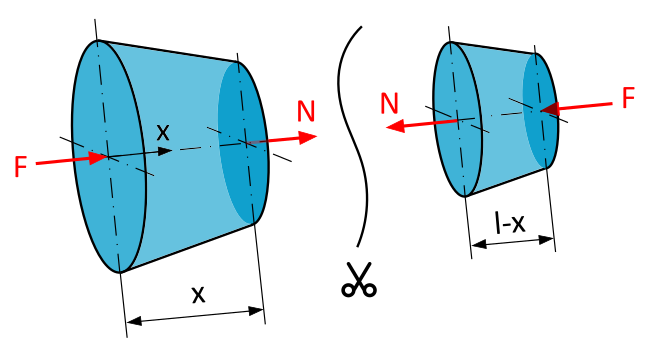
Da der Stab im Gleichgewicht ist (d.h. er bewegt sich nicht), müssen die Kräfte in x-Richtung gleich sein.
Stellen wir jetzt die horizontale Gleichgewichtsbedingung für beispielsweise unseren linken Schnitt auf können wir damit die Normalkraft \(N\) bestimmen:
Also: N = -F. Das bedeutet, die Normalkraft ist negativ, weil sie der Druckkraft entgegenwirkt. Also wirkt sie genau andersherum, als wir es uns in der Abb. B2 eingezeichnet haben.
Wir erhalten also eine konstante (da von \(x\) unabhängige), negative, innere Normalkraft, d.h. wir haben eine Druckkraft und somit nach Gleichung 1.3/1.3b eine Druckspannung. Dies muss so sein, da die Fläche positiv ist und negative Kraft durch positive Fläche eine negative Spannung (= Druckspannung) ergibt.
Ganz einfach: Am Stabanfang wirkt eine äußere Kraft auf unseren Stab. Da bis zum Stabende keine Änderung dieser Kraft durch weitere äußere Kräfte eintritt, bleibt auch die Normalkraft über den ganzen Stab konstant.
Schritt 2: Fläche in Abhängigkeit von \(x\) bestimmen
Da es sich um einen konischen Stab handelt, ist die Schnittfläche im senkrechten Schnitt zur Stabsachse stets kreisförmig. Die Formel für eine Kreisfläche lautet:
Wie oben bereits angemerkt, besteht der Schwierigkeitsgrad dieser Aufgabe darin, dass die Querschnittsfläche \(A\) des Stabes konisch und damit für jede Position \(x\) unterschiedlich ist. Wenn wir uns das Problem in einer Grafik ansehen, erkennen wir schnell, dass wir den Radius \(r\) in Abhängigkeit von der Position \(x\) darstellen müssen, um diese Aufgabe zu lösen:
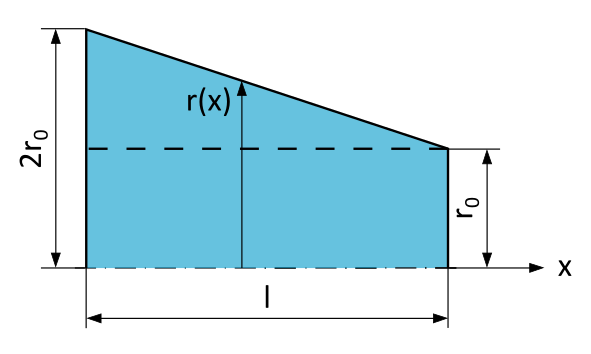
Wir suchen also \(r(x)\), um die Fläche wie folgt beschreiben zu können:
Ein solches Problem können wir auf mindestens zwei verschiedene Wege lösen. Entweder wenden wir den 2. Strahlensatz an oder wir stellen die Funktionsgleichung der Geraden \(r(x)\) auf.
Beide Wege führen natürlich zum exakt gleichen Ziel. Welchen man nimmt, hängt selbstverständlich davon ab, welcher der beiden Rechenwege einem am meisten liegt. Daher sehen wir uns an dieser Stelle beide Möglichkeiten genauer an.
Weiterlesen mit TechMechAcademy+
Alles. Immer. Überall.
Mit TechMechAcademy+ vollen Zugriff auf alle Inhalte.
Die Vorteile im Überblick:
- Kostengünstigstes Angebot.
- Ideal, wenn du für kurze Zeit Zugriff auf bereits identifizierte Inhalte benötigst.
- Unbegrenzter Zugriff auf alle vorhandenen und neu erstellten Inhalte während der gesamten Premiummitgliedschaft.
- Garantierte Premiummitgliedschaft für 24 Stunden. Der Zugang endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag. Keine Kündigung notwendig.
3,99 €
Die Vorteile im Überblick:
- Kostengünstiges Angebot.
- Ideal für kurzfristige Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
- Unbeschränkter Zugang zu sämtlichen bestehenden und frisch erstellten Inhalten im Rahmen der gesamten Premiummitgliedschaft.
- Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einer Woche gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag der Folgewoche. Keine Kündigung notwendig.
9,99 €
Die Vorteile im Überblick:
- Profitiere vom Bestseller.
- Ideal für effektive Prüfungsvorbereitung mit den Inhalten von TechMechAcademy.
- Unlimitierter Zugriff auf alle bereits vorhandenen und neu geschaffenen Inhalte während der gesamten Dauer der Premiummitgliedschaft.
- Die Premiummitgliedschaft ist für einen garantierten Zeitraum von einem Monat gültig. Der Zugang beginnt am Tag der Aktivierung und endet automatisch um 0:00 MEZ (Mitteleuropäische Zeit) am darauffolgenden Tag des Folgemonats. Keine Kündigung notwendig.
14,99 €
Bist du bereits ein TechMechAcademy+ Premiummitglied? Dann logge dich bitte hier ein, um den vollen Zugriff auf alle Inhalte zu genießen.
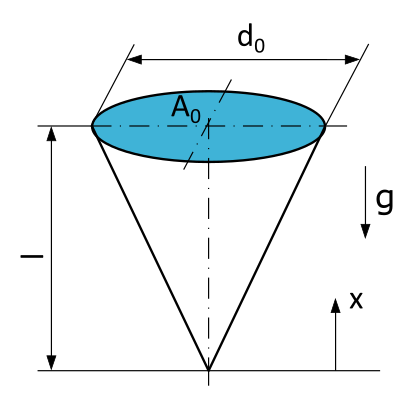
Hängender Kreiskegel
An einer Dachrinne hängt ein Eiszapfen. Der Zapfen besitzt die Form eines Kreiskegels mit der Länge \(l=10~\mathrm{cm}\), der am Aufhängepunkt einen Durchmesser \(d_0=5~\mathrm{cm}\) und eine Querschnittsfläche \(A_0\) hat. Das Eis hat eine Dichte von \(\varrho = 0,91~\mathrm{g/cm^3}\).
- Wie lautet die Formel zur Berechnung der Normalkraft \(N\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Kegelachse?
- Wie lautet die Formel zur Berechnung der Normalspannung \(\sigma\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Kegelachse?
- Wie groß ist die Normalspannung \(\sigma\) an der Stelle \(x=70~\mathrm{mm}\) in einem Schnitt senkrecht zur Kegelachse?
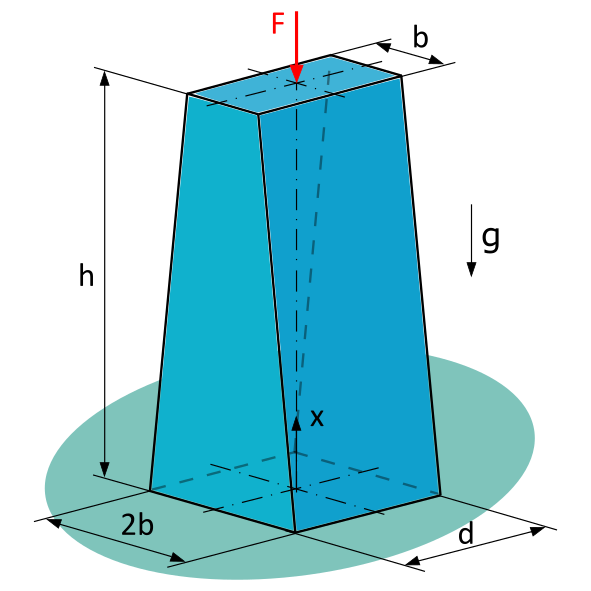
Belasteter homogener Stab mit konstanter Dicke und linear veränderlicher Breite
Ein homogener Stab mit konstanter Dicke \(d=20~\mathrm{mm}\) und linear veränderlicher Breite wird durch eine Druckkraft \(F=1~\mathrm{kN}\) belastet.
Geg.: \(b=15~\mathrm{mm}\), \(h=80~\mathrm{mm}\), \(\varrho = 7,85~\mathrm{g/cm^3}\)
- Wie lautet die Formel zur Berechnung der Querschnittsfläche \(A(x)\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Stabachse?
- Wie lautet die Formel zur Berechnung der Normalkraft \(N(x)\) an einer beliebigen Stelle x in einem Schnitt senkrecht zur Stabachse?
- Wie groß ist die Normalspannung \(\sigma\) an der Stelle \(x=30~\mathrm{mm}\) in einem Schnitt senkrecht zur Stabachse?


