2.2 Normal- und Schubspannungen unter einem beliebigen Schnittwinkel
Im letzten Abschnitt haben wir gelernt, wie man die Normalspannung berechnet, wenn der Schnitt senkrecht zur Stabachse verläuft. Aber was ist, wenn der Schnitt schräg verläuft?

Klar, zwei Schnitte senkrecht zur Achse sind easy. An beiden Seiten hast du dann die gleiche Normalkraft \(N_x\). Sozusagen: Alles im Lot, alles easy.

Aber wird's nicht komplizierter, wenn du den Schnittwinkel beliebig wählst? Nö! Denk dran: Das System will im Gleichgewicht bleiben. Sonst würde der abgeschnittene Teil abhauen – und wo kämen wir denn da hin?
Also: Egal wie du schneidest, die Kraft auf der Stabsachse muss beim einachsigen Spannungszustand in beide Richtungen gleich sein. Sonst würde sich der ganze Kram bewegen!
Ach ja, und der Spannungsvektor? Der zeigt dir immer schön an, wo's lang geht. Bei gleichmäßiger Verteilung der inneren Kräfte liegt er brav auf der x-Achse. Daneben gibt's noch seine Komponenten Normal- und Schubspannung, aber die sind entweder im rechten Winkel zur Schnittfläche (normal, oder?) oder liegen in der Schnittfläche.
Damit ist klar: Im geraden Schnitt gibt es bei einachsiger Beanspruchung keine Schubspannung, da der Spannungsvektor nur aus der Komponente Normalspannung besteht.
Warum? Na klar, Spannungsvektor und seine Komponente Normalspannung liegen auf der x-Achse! Es gibt kein Spannungsdreieck. Also ist die Schubspannung Null.
Stellen wir uns vor, wir haben eine coole Schnittfläche und wollen wissen, wie die Spannungen dort verteilt sind. Dazu müssen wir die Koordinatenachse so drehen, dass sie senkrecht zur Schnittfläche steht. So entsteht unsere neue \(\xi\)-Achse (\(\xi\) ist übrigens der griechische Buchstabe 'xi').
Der Schnittwinkel \(\varphi\) (vgl. Abb. 1.2.3, Abb. 1.2.4) ist sozusagen der Winkel zwischen der alten x-Achse und unserer neuen \(\xi\)-Achse. Quasi eine Drehung der x-Achse, um die ganze Sache einfacher zu machen.

Ganz einfach: Mit dieser Drehung können wir die Normal- und Schubspannung mithilfe eines Kräftedreiecks berechnen. Das ist ein super praktisches Werkzeug, um Spannungen zu analysieren.
Im Kräftedreieck sehen wir drei wichtige Kräfte:
- Die Resultierende \(N_x\): Das ist die Kraft, die alles zusammenhält. Richtung des Spannungsvektors. Im Dreieck die Hypothenuse, also gegenüber des rechten Winkels.
- Die Normalkraft \(N_{\xi}\): Sie wirkt senkrecht zur Schnittfläche und drückt/zieht die beiden Schnittflächen gegen- bzw. auseinander, abhängig von der vorherrschenden Belastung (Zug/Druck).
- Die Querkraft \(Q_{\eta}\): Sie wirkt parallel zur Schnittfläche und versucht, die beiden Schnittflächen gegeneinander zu verschieben.

Du erinnerst dich vielleicht noch an die Vorzeichenfestlegung für Normal- und Schubspannungen? Da haben wir gelernt, dass die Normalspannung positiv ist, wenn sie in die gleiche Richtung wie die \(\xi\)-Achse zeigt. Aber die Schubspannung ist ein sneaky Biest! Sie kann mal positiv und mal negativ sein, je nachdem, wie wir unsere Koordinatenachsen ausrichten.
Um das wahre Gesicht der Schubspannung zu entlarven, brauchen wir eine weitere Achse: die \(\eta\)-Achse (\(\eta\) ist übrigens der griechische Buchstabe 'eta'). Diese Achse liegt in der Schnittfläche und ist senkrecht zur \(\xi\)-Achse.
Wo genau die \(\eta\)-Achse liegt, hängt davon ab, welches Koordinatensystem wir vor dem Schnitt verwendet haben. Keine Sorge, das ist meistens gar nicht so schwer zu erkennen!
Sobald wir die \(\eta\)-Achse haben, können wir endlich die Schubspannung berechnen und ihr wahres Vorzeichen bestimmen.
Aber Achtung: Das Vorzeichen der Schubspannung ändert nichts an ihrer physikalischen Eigenschaft. Egal ob positiv oder negativ, sie beschreibt immer noch die gleiche Kraft, die versucht, die beiden Flächen gegeneinander zu verschieben.
Daher kann es uns eigentlich völlig egal sein - wären da nicht die Klausuren, bei denen das richtige Vorzeichen der Schubspannung Punkte bringen kann.
Du kennst das bestimmt: Manchmal ist es einfach einfacher, die Dinge aus einem anderen Blickwinkel zu betrachten. Genauso ist es auch mit der Schubspannung!
Nehmen wir zum Beispiel das übliche x,y-Koordinatensystem:
- x-Achse: Nach rechts ist positiv.
- y-Achse: Nach oben ist positiv.

Was passiert jetzt, wenn wir unser Koordinatensystem um den Schnittwinkel \(\varphi\) drehen?
- Die Schubspannung \(\tau_{\xi\eta}\) (\(\xi\)-\(\eta\)-Komponente), die aus der Querkraft \(Q_{\eta}\) hervorgeht, hat die gleiche Richtung wie die negative \(\eta\)-Achse.
- Da die \(\eta\)-Achse nach links oben positiv ist, ist die Schubspannung in diesem Fall negativ.
Aber keine Sorge! Das ändert nichts an der physikalischen Bedeutung der Schubspannung. Sie beschreibt immer noch die gleiche Kraft, die versucht, die beiden Flächen gegeneinander zu verschieben.
- x-Achse: Nach rechts ist positiv.
- z-Achse: Nach unten ist positiv.

Diesmal ist die Schubspannung \(\tau_{\xi\eta}\) wie die Querkraft \(Q_{\eta}\) positiv, weil sie mit der positiven \(\eta\)-Achsenrichtung zusammenfällt.
- Das Vorzeichen der Schubspannung hängt vom gewählten Koordinatensystem ab.
- Die physikalische Bedeutung der Schubspannung bleibt jedoch immer gleich.
Wir wollen die Normal- und Schubspannung unter einem beliebigen Schnittwinkel berechnen. Dazu brauchen wir:
- Die Normalkraft \(N_x\) in Richtung der x-Achse.
- Die Schnittfläche \(A\) des Schnittes senkrecht zur x-Achse.
- Den Schnittwinkel \(\varphi\).
- Die Kräfte \(N_{\xi}\) und \(Q_{\eta}\) in der \(\xi\)-\(\eta\)-Ebene.
- Die Schnittfläche \(A^*\)
Das bedeutet:
\(N_{\xi}\), \(Q_{\eta}\) und \(A^*\) als Funktionen des Schnittwinkels \(\varphi\) darstellen.
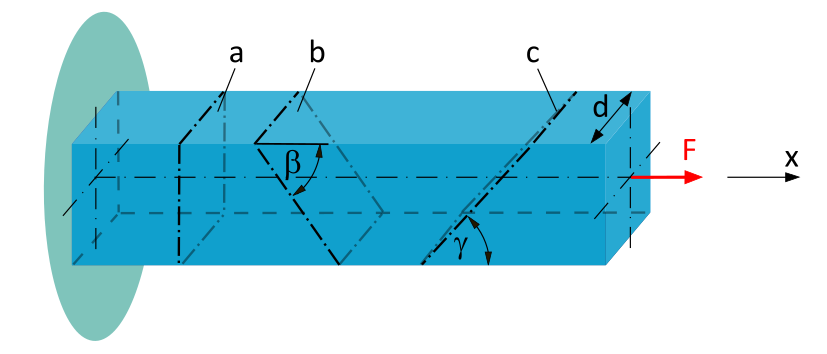
Normal- und Schubspannung unter beliebigem Schnittwinkel
Ein eingespannter Balken mit quadratischem Querschnitt (Seitenlänge \(d=20~\mathrm{mm}\)) wird durch eine Zugkraft \(F=10~\mathrm{kN}\) in der Balkenachse belastet.
Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die
- in der Schnittebene a wirken.
- in der Schnittebene b (\(\beta = 50°\)) wirken.
- in der Schnittebene c (\(\gamma = 40°\)) wirken.