2.3.3 Ablesen der Spannungen am Mohr'schen Spannungskreis
Im vorherigen Abschnitt haben wir erarbeitet, wie wir den Mohr'schen Spannungskreis zeichnen können, wenn uns die Normalspannung \(\sigma_x\) bekannt ist. Jetzt lernen wir, wie wir aus dem Mohr'schen Spannungskreis für den einachsigen Spannungszustand Spannungen unter beliebigem Schnittwinkeln ablesen können.
Bevor wir uns damit beschäftigen, wie wir die Werte am Mohr'schen Spannungskreis ablesen können, zunächst zwei Anmerkungen:
Anmerkung 1: Der Schnittwinkel wird im Spannungskreis mit dem doppelten Winkel eingezeichnet/abgelesen!
Bei der Herleitung der Kreisgleichung für den Spannungskreis haben wir die Ausgangsformeln (1.4) und (1.5xy) bzw. (1.5xz) verwendet, die den doppelten Schnittwinkel \(2\varphi\) enthalten.
Entsprechend wird der Schnittwinkel im Mohr'schen Spannungskreis mit dem doppelten Winkel abgelesen bzw. eingezeichnet.
Anmerkung 2: Zählrichtung des Winkels \(2\varphi\) im Mohrschen Spannungskreis
Während der Schnittwinkel \(\varphi\) in den möglichen \(x\), \(y\)- oder \(x\), \(z\)-Koordinatensystemen am Bauteil gegen den Uhrzeigersinn positiv gezählt wird (vgl. Rechte-Hand-Regel im kartesischen Koordinatensystem + Rechte-Daumen-Regel zur Bestimmung der positiven Drehrichtung), hängt die Zählrichtung des Winkels \(2\varphi\) im Mohrschen Spannungskreis sowohl vom verwendeten Koordinatensystem (vgl. Abb. 1.2.6, Abb. 1.2.7) als auch von der Wahl des \(\tau\)-Achsenverlaufes (vgl. Abb. 1.2.15) ab.
Man kann die positive Drehrichtung des Winkels \(2 \varphi\) im Mohr'schen Spannungskreis für eine gewünschte Kombination aus verwendetem Koordinatensystem + \(\tau\)-Achsenverlauf bestimmen, indem man abhängig vom verwendeten Koordinatensystem die Formel 1.5xy oder 1.5xz nimmt und eine beliebige positive oder negative Normalspannung \(\sigma_x\) und den positiven Schnittwinkel \(\varphi = 45°\) einsetzt.
Da \(\sin(2\cdot45°) = \sin(90°) = 1\) gilt, kann die Schubspannung für diesen Winkel leicht bestimmt werden: \(\tau = -\frac{\sigma_x}{2}\) im \(x\),\(y\)-Koordinatensystem und \(\tau = \frac{\sigma_x}{2}\) im \(x\),\(z\)-Koordinatensystem.
Skizziert man nun das \(\tau\),\(\sigma\)-Koordinatensystem mit dem gewünschten \(\tau\)-Achsenverlauf positiv nach oben oder unten und trägt die verwendete Normalspannung \((\sigma_x|0)\) und die berechnete Schubspannung \((\frac{\sigma_x}{2}|\tau)\) auf, dann ist die positive Zählrichtung der kürzeste Winkelbogen von \((\sigma_x|0)\) zu \((\frac{\sigma_x}{2}|\tau)\), da dies die in die Gleichung 1.5xy bzw. 1.5xz eingesetzten \(2 \cdot \varphi = +90°\) sein müssen.
Beispiel (vgl. Tabelle 1.2.1, Nr. 1):
- \(x\), \(y\)-Koordinatensystem
- \(\tau\)-Achsenverlauf nach oben positiv
Gewählt: \(\sigma_x = 30~ \mathrm{N/mm^2}\)
Berechnet: \(\tau = - \frac{\sigma_x}{2}\cdot 1 = -15~ \mathrm{N/mm^2}\)
Skizze:
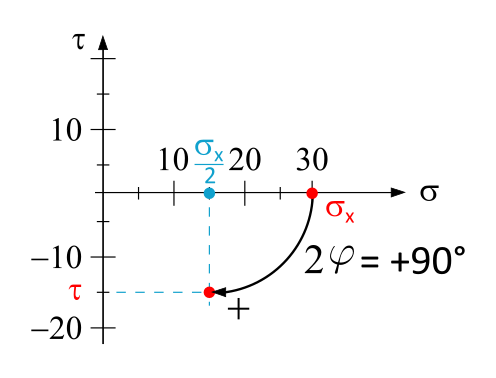
Also ist die positive Zählrichtung des Winkels \(2\varphi\) im Uhrzeigersinn in einem Mohrschen Spannungskreis mit einer nach oben positiv verlaufenden \(\tau\)-Achse und unter Anwendung des \(x\), \(y\)-Koordinatensystems (\(y\)-Achse nach oben positiv) für den Schnittwinkel am Bauteil.
Diese positive Zählrichtung gilt natürlich für alle Mohrschen Spannungskreise, die diesen Verlauf der \(\tau\)-Achse kombiniert mit dem \(x\), \(y\)-Koordinatensystem (mit \(y\)-Achse nach oben positiv) am Bauteil verwenden.
Die folgende Tabelle zeigt, welche Drehrichtung des Winkels \(2\varphi\) im Mohrschen Spannungskreis bei einer beliebigen Kombination aus verwendetem Koordinatensystem und \(\tau\)-Achsenverlauf positiv gezählt wird:
Positive Zählrichtung des Winkels \(2\varphi\) im Mohrschen Spannungskreis
| Nr. | Koordinatensystem | \(\tau\)-Achsenverlauf | Positive Zählrichtung | ||
| 1 |  |
\(+\) |  |
\(\Rightarrow\) |  |
| 2 |  |
\(+\) |  |
\(\Rightarrow\) |  |
| 3 |  |
\(+\) |  |
\(\Rightarrow\) |  |
| 4 |  |
\(+\) |  |
\(\Rightarrow\) |  |
Was kann man ganz allgemein am Mohrschen Spannungskreis ablesen?
Die maximale und die minimale Normalspannung, die im gegebenen Spannungszustand auftreten können, sind die beiden Schnittpunkte des Spannungskreises mit der \(\sigma\)-Achse.
Für eine Zugspannung ist also die maximale Normalspannung \(\sigma_x\) und die minimale Normalspannung \(0\), während für eine Druckspannung die maximale Normalspannung \(0\) und die minimale Normalspannung \(\sigma_x\) ist.
Der Zählbeginn des Winkel \(2\varphi\) ist jeweils an der angetragenen Normalspannung \(\sigma_x\). Dies muss so sein, da hier der Schnittwinkel am Bauteil \(\varphi = 0°\) sein muss.
Also bekommen wir für Zug- und Druckbelastung die Normalspannung \(0\), wenn wir im Spannungskreis den Winkel \(2\varphi = 180°\) abgreifen. Dies entspricht wegen dem doppelten Winkel im Spannungskreis am Bauteil einen Winkel von \(90°\).
Die letzte allgemeine Information aus dem Spannungskreis ist, dass der Betrag der maximalen Schubspannung \(|\tau_{max}|\) dem Kreisradius \(|\frac{\sigma_x}{2}|\) entspricht.
Ablesebeispiel für einen Schnittwinkel \(\varphi = 67,5°\)
Wir suchen für das am häufigsten verwendete \(x\), \(y\)-Koordinatensystem mithilfe von zwei Mohrschen Spannungskreisen (einmal \(\tau\)-Achsenverlauf positiv nach oben und einmal \(\tau\)-Achsenverlauf positiv nach unten):
- für eine Zugspannung \(\sigma_x=200~\frac{\mathrm{N}}{\mathrm{mm^2}}\) die bei einem Schnittwinkel von \(\varphi = 67,5°\) auftretende Normal- und Schubspannung
- für eine Druckspannung \(\sigma_x=-200~\frac{\mathrm{N}}{\mathrm{mm^2}}\) die bei einem Schnittwinkel von \(\varphi = 67,5°\) auftretende Normal- und Schubspannung
Zunächst zeichnen wir die Spannungskreise entsprechend der uns bekannten 4 Schritte:
- Zeichnen der vier \(\sigma\), \(\tau\)-Koordinatensysteme: Die \(\sigma\)-Achse verläuft immer horizontal nach rechts, die \(\tau\)-Achse je zweimal vertikal nach oben positiv und zweimal vertikal nach unten positiv.
- Die Normalspannung \(\sigma_x\) wird auf der \(\sigma\)-Achse unter Beachtung ihres Vorzeichens eingezeichnet. Wähle einen geeigneten Maßstab, der für die \(\sigma\)- und die \(\tau\)-Achse gleich sein muss, beispielsweise \(1 ~\mathrm{cm}\) pro \(50 ~\frac{\mathrm{N}}{\mathrm{mm^2}}\).
- Mittig zwischen \(\sigma_x\) und der \(\tau\)-Achse liegt der Kreismittelpunkt \(\frac{\sigma_x}{2}\).
- Damit kann der Spannungskreis mit einem Zirkel gezeichnet werden.
Nun können wir die gesuchten Normal- und Schubspannungen ablesen. Beachte dabei die Zählrichtung des Winkels \(2 \varphi\) für die verwendeten Spannungskreise (siehe Tabelle 1.2.1) und den Umstand, dass der Zählbeginn des Winkels \(2 \varphi\) jeweils an der angetragenen Normalspannung \(\sigma_x\), egal ob Zug- oder Druckspannung, ist. Denn hier ist der Schnittwinkel \(\varphi = 0°\).
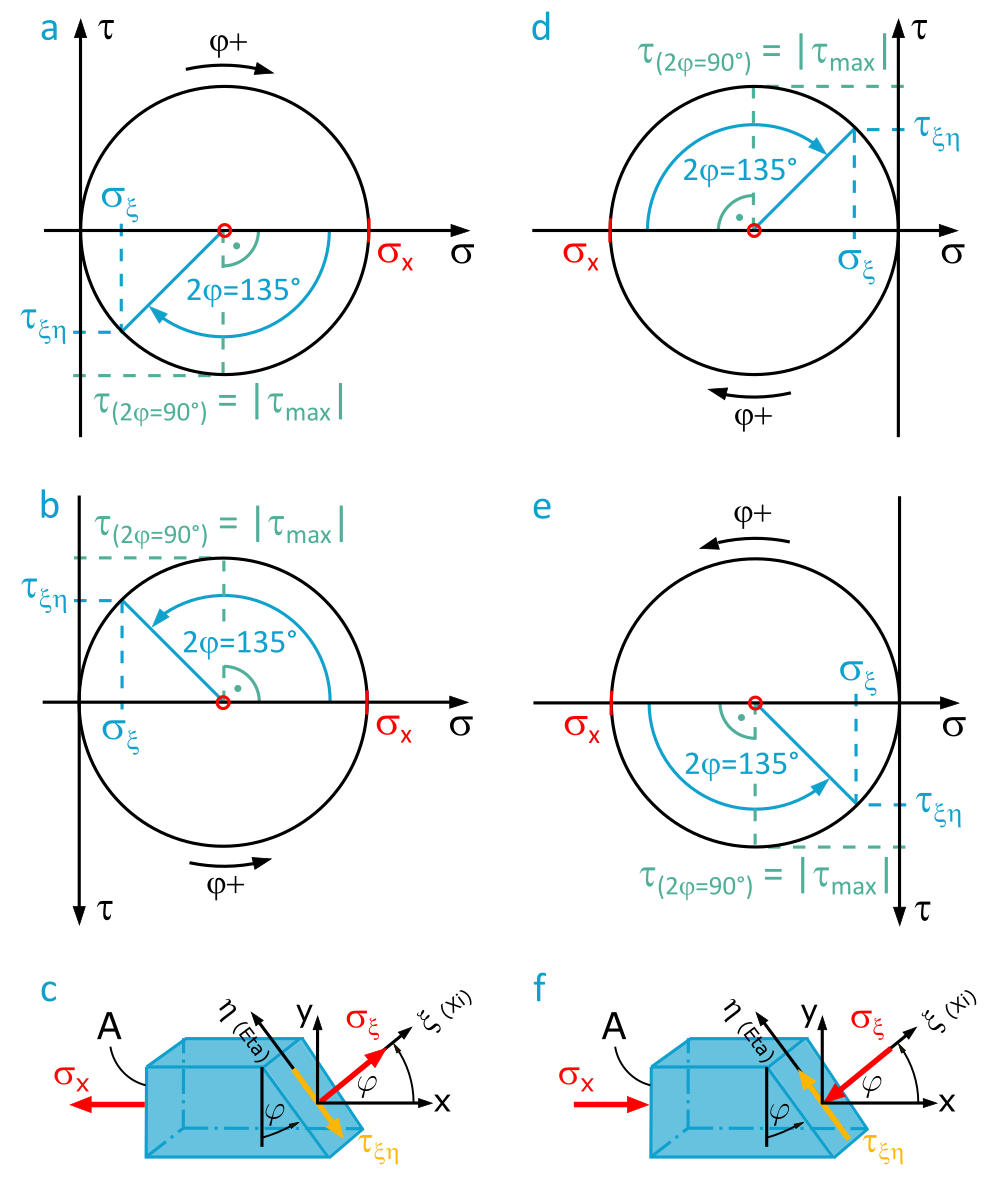
Die Abbildung 1.2.17 zeigt die Ableseergebnisse für einen Schnittwinkel \(\varphi = 67,5°\), d.h. \(2\varphi = 135°\):
- Für eine Zugspannung \(\sigma_x = 200~\frac{\mathrm{N}}{\mathrm{mm^2}}\) (a, b,
c) :
\(\sigma_{\xi} = +29 ~\frac{\mathrm{N}}{\mathrm{mm^2}}\), \(\tau_{\eta\xi} =-70 ~\frac{\mathrm{N}}{\mathrm{mm^2}}\) - Für eine Druckspannung \(\sigma_x = -200~\frac{\mathrm{N}}{\mathrm{mm^2}}\) (d, e,
f) :
\(\sigma_{\xi} = -29 ~\frac{\mathrm{N}}{\mathrm{mm^2}}\), \(\tau_{\eta\xi} = +70 ~\frac{\mathrm{N}}{\mathrm{mm^2}}\)
Unter Beachtung von Zählbeginn und Zählrichtung des Winkels \(2\varphi\) wird deutlich: Der Betrag der maximalen Schubspannung \(|\tau_{max}| = |\frac{\sigma_x}{2}|\) tritt im 45°-Schnitt (\(2\varphi=90°\)) zur angreifenden Belastung auf.