Für welche Schnittwinkel \(\varphi\) sind die Normalspannung \(\sigma_\xi\) und die Schubspannung \(\tau_{\xi\eta}\) maximal?
Jetzt geht's darum, wann die Normalspannung und die Schubspannung im einachsigen Spannungszustand am größten sind. Also, schnall dich an, es wird spannend!
- An einem Ende wird er gedehnt oder gestaucht.
- Im Inneren des Stabs herrschen dann Spannungen.
- Diese Spannungen können wir in Normalspannungen und Schubspannungen zerlegen.
Um uns die Lösung zu verdeutlichen, kramen wir erstmal die in den vorherigen Schritten entwickelten Formeln für Normalspannungen und Schubspannungen hervor:
(1.4)
-
\(x\),\(y\)-System
$$ \begin{aligned} \tau_{\xi\eta} = -\dfrac{\sigma_x}{2}\bigl(\sin(2\varphi)\bigr) \end{aligned} $$
(1.5xy)
-
\(x\),\(z\)-System
$$ \begin{aligned} \tau_{\xi\eta} = \dfrac{\sigma_x}{2}\bigl(\sin(2\varphi)\bigr) \end{aligned} $$
(1.5xz)
Interessant: Die Schnittwinkel \(\varphi\), bei denen die Normal- und Schubspannung jeweils maximal werden, treten in der Sinus- und in der Kosinusfunktion auf.
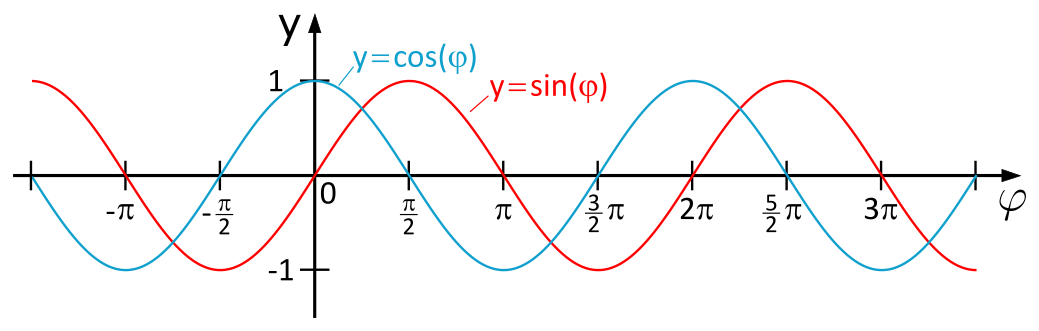
Für unseren Schnittwinkel \(\varphi\) ist eigentlich nur ein kleiner Ausschnitt der Abbildung interessant: der zwischen \(\varphi=0\) (senkrechter Schnitt) und \(\varphi=90°\), was im (Bogenmaß) \(\varphi=\frac{\pi}{2}\) entspricht.
- die Sinuskurve erreicht ihren Minimalwert von 0 bei \(\varphi=0\) und ihren Maximalwert von 1 bei \(\varphi=\frac{\pi}{2}\).
- die Kosinuskurve erreicht ihren Minimalwert von 0 bei \(\varphi=\frac{\pi}{2}\) und ihren Maximalwert von 1 bei \(\varphi=0\).
- In Gl.(1.4) finden wir den Kosinus - der ist maximal, wenn sein Argument 0 ist, also für \(\varphi=0\).
- Also ist die Normalspannung am größten, wenn du den Stab quer durchschneidest.
- Also genau senkrecht zur Stabachse.
- In diesem Fall ist die Schubspannung gleich null.
- Kannst du dir das vorstellen? Sozusagen der "stärkste" Schnitt.
- In Gl.(1.5xy) und (1.5xz) finden wir den Sinus - der ist maximal, wenn sein Argument \(\frac{\pi}{2}\) ist.
- Vorsicht, Falle! Da der Winkel \(\varphi\) als Argument nicht alleine, sondern mit dem Faktor 2 vorkommt, gilt in diesem Fall nicht \(\varphi=\frac{\pi}{2}\), sondern \(\varphi=\frac{\pi}{4}\)!
- Also ist die Schubspannung am größten, wenn du den Stab in einem Winkel von 45 Grad zur Stabachse durchschneidest.
- Merke dir: 45 Grad ist die magische Zahl!
- In diesem Fall ist die Normalspannung halb so groß wie die maximale Normalspannung.
- Maximale Normalspannung
- Senkrechter Schnitt zur Stabachse
- Schubspannung gleich null
- Maximale Schubspannung
- Schnittwinkel von 45 Grad zur Stabachse
- Normale Spannung halb so groß wie maximale Normalspannung
Beim einachsigen Spannungszustand tritt der Betrag der maximalen Normalspannung \(\lvert \sigma_{max} \rvert = \lvert \sigma_{x} \rvert\) im senkrechten Schnitt und der Betrag der maximalen Schubspannung \(\lvert \tau_{max} \rvert = \lvert \frac{\sigma_{x}}{2} \rvert\) im 45°-Schnitt \(\bigl(\frac{\pi}{4}\bigr)\) zur angreifenden Belastung auf.
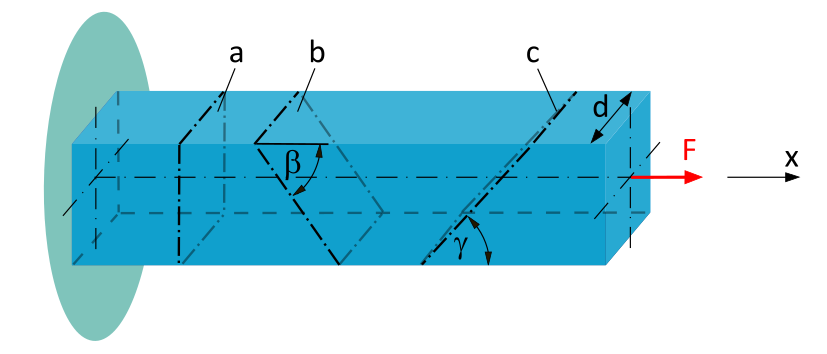
Normal- und Schubspannung unter beliebigem Schnittwinkel
Ein eingespannter Balken mit quadratischem Querschnitt (Seitenlänge \(d=20~\mathrm{mm}\)) wird durch eine Zugkraft \(F=10~\mathrm{kN}\) in der Balkenachse belastet.
Bestimme die mittlere Normalspannung und die mittlere Schubspannung, die
- in der Schnittebene a wirken.
- in der Schnittebene b (\(\beta = 50°\)) wirken.
- in der Schnittebene c (\(\gamma = 40°\)) wirken.